0000024

Szkieletem    grofu C nazywany graf zwykły

C₀. mejęcy ton sam zbiór wierzchołków i którego krawędzie łęczę to i tylko te różno wierzchołki, które eę przyległo w grafie G. Kocierz przylogłoóci wierzchołków ezkielotu grafu Jeot równa binarnej macierzy przylogłoóci wierzchołków grafu wtody i tylko wtody, gdy graf ten nie ma pętli.

Szkieletem    hipergrafu H ■ <X,U,P>

nazywany hipergrof zwykły, boz hiporkrewędzi Jednoczłonowycb.

H_ft • <X,U_o,P_o> *    U_B jeot zbiorem hiperkrowędzi, co naj -

mniej dwuczłonowych, okreólonyn następujęco

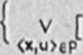
u C U a x / <x

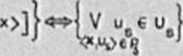
Szkielot hiporgrafu Jeot noónikiem informacji o przylogłoóci różnych wierzchołków tego hiporgrafu i Jago opójnoóci.

Elemonty macierzy przylogłoóci wierzchołków ezkielotu gra-fu (hiporgrafu) i binernoj macierzy przylogłoóci wiorzchołków grofu (hipergrafu) eę tobie równe, zo wyjętkien elemontów główno j przokętnoj, które dla ezkiolotu tę równo zoru.

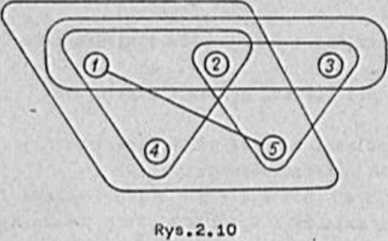
Szkło lot grafu z ryo.2.3 Jeot przedstawiony na ryo.2.9. a ezklelet hiporgrafu z przykładu 2.1 przedstawiono na ryo.2.10.

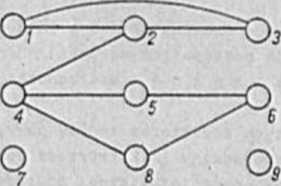
Ryo.2.9

Przykład 2.6

Oodnę z możliwych interpretacji fizycznych liczby podziel-noócl dostarcza następująca eytuacja:

□oot dziewięć odczynników chemicznych roagujęcych zo oobę w różny opooób. Niech odczynniki te będę roprezentowonc wiorz-chołkomi grofu z ryo.2.3. Różno rodzaj© rookcji chomicznych ro-prozontuję gałęzie togo grofu. Substancjo połączono gołęzię nlo mogę być przochowywone w tym eomys pomioozczenlu. Nałoży okreó-lić najmniojezę lloóć pomiotzczoń magazynowych, niezbędnych do przechowywania tych odczynników oraz przydziolić odczynniki do tych pomioozczeń.

.•.'yctarczojocyn, z punktu widzonio colu nodolowonio, oodolea oy-etonowym naozogo obioktu zointereoowoó joot strukturo przedstawiono grafem z ryo.2.3. lloóć pomioozczoń magazynowych joot równo liczbie podzielnoóci grofu p(G) • 3, o podzbiory odczynników przochowywonych w poozczogólnych pomieszczeniach oę na przykład następująco {1,4,7} , {2,5,8} , {3,6,9} .

Oczywiście można inoczoj podzlolić odczynniki no trzy rozłęczno podzbiory, locz ilość tych podzbiorów będzio zowszo nio mnioj -oza niż p(G).

2.6. Izomorfizm grofów

Owo grofy Identyczne w owoj istocie mogę się formalnie różnić z powodu innych nazw wiorzchołków i gałęzi. Zmieniając więc odpowiednio nazwy wierzchołków i gałęzi, możemy uzyekoć Jeden i ten oom graf. Grofy tokio oę nozywone izomorficznymi. Formolnie G ■ <X,U,P> i H« <W,V,R) oę izomorficzno wtoay i tylko wtody, gdy iotnloję dwo wzojoanie Jednoznaczne przokoztołconio: «X t X-*W oroz p, * u-«^V takie, że prowdziwo joot nootępujęce zdonie

A A r<x.y.u> €    <a(x), «(y). fo(u)> CR]

x,y€X utu

47