0000022 2

Dopełnieniom C_d grafu G • <X,U,P> t G( A.O.C) (do grafu polnego) nazywany graf C_d ■<X.U_d,P_d> toki, że

C_d€ 0( A,O.C)

oraz

“o ■ ^up\^u- % • ^pP\^p

InoczoJ mówięc, dopołnionio C_d grafu C Jeat grofem o tyn ooaya zbiorzo wierzchołków, zowierajęcyn te gałęzie, które wyotępuję w grafie pełnym toj klooy, o nie na ich w grofio C. W myśl tej dofinicji dopołnionio dopołnionio G_d Jeat grafom C. Analogicznie zdefiniowane Jeot dopołnionio hiporgrafu.

Grof Zwykły

G€ 0(1.0,0)

Grof B e r g e' o [4]

G CG(O.i.l)

M u 1 t igr U n i g r a f

a f - kaZdy toki graf. dlo którego K(G)>1. - keZdy taki graf, dla którogo K(G) ( 1.

2.4.1. Rodzaje grafów Borgo'e

Kaidy grof 5orgo*o, GCC(O.l.l). C • <X,U'.P> , Joot izo -morficzny z odpowiednio relacjo dwuczłońowę, okreólono w zbiorze wierzchołków, U cx«X, przy czyn U w u' oraz u’ * P. Można zatoa uproóclć zaplo tego grafu do poatacl dwójki uporzędkowo-noj G ■ <X, U> , ponieważ w zapleie G • <X,u',P> relacja P na tę wleenoóć, to -dla każdej gałęzi uf U¹ latnleje dokłodnie Jod-no paro uporzodkowana <x,y>£XxX taka,' że <x,y,u> 6P. Możno również, zależnlo od wygody zapleu, etoeowoć notację C»4X,r> lub G »<X, P"^ł> , gdzie r oraz r”¹ aę okroólone noetępujęco

r«X-^2^X; gdzie T(x) .{yfX i J^t.y.u) tp)

r"^ł « X — 2^X; gdzie r"^ł(x) - I z €X : V<z.x.u> £ p)

»    utU

B

Zbiór P(x) będziemy nozywoli zbiorem "nootępników" wlorzchoł-ko x, notooieot r^-1(x) zbiorom "poprzedników" wiorzchołko x.

Przykład 2.6

Grof Borge*o przedstawiony ni» ryo.2.6

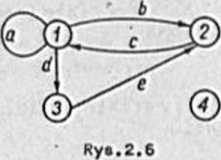
oote być zepioony nootępujęcot 1/ C • < X, U > , gdzie X - {1.2.3.4} ,

U - {o.b.c.d.o] - {<1.1> . <1.2> . <2.1>. <1,3> . <3,2>}; 2/    C-<X.P>, gdzie

X - { 1.2.3.4] ;

Pl P(l) - {1.2.3} . P( 2) • {1} . P( 3) - {2}. P( 4) . p 3/ G - < X. r*^ł >, gdzie X - {l.2.3,4} ,

r-¹ : P"^ł(i) - {1.2} , r“¹ (2) . {1.3} . r"¹(3) -{1}. r'^4) - JJ.

Z punktu widzenie właonoóci rolocji dwuczłonowoJ UCX “X, izomorficznej z grafom Oorgo'o. G • <X,P> wyróżnię eię neotępu -Jęce rodzaje grafów Borgo'at

-    zwrotny

A^,£r<^x>

-    przoclwzwrotny

A x* T(x) xfX

-    cymo t ryczny

A [ycn|x)-fKtP(y)]

<x^>tX*X    ^J

m