0000055 2

Rozdział 7

CYKLOMATYKA GRAFÓW I HIPERGRAFÓA

7.1. Liczba cyklomatyczno

Weźmiemy pod uwagę dowolny hlpergraf H • <X,U.P> ,

|X| ■ n, IU|■ m. Ilość okładowych spójności oznaczona Jeet Jako X • Określimy funkcję k :    w naetępujęcy apoeób:

Niech Uj € U,

x

<X. Uj> C PAX-

M“j) - Mi)

Wartość k(Uj) określa ilu członowa Jeot relacja R. której element X reprezentuje hipergołęż u^.

W przypadku gdy H Jeet grafem, to

A k( u) • 2

.CII '    *

Liczba cyklomatyczna A(H) będzie zdefl -nlowana naotępujęco

Ola grafu G otrzymany konsekwentnie

A(G) > a ♦ K - n

Przykłod 7.1

Wyznaczyey liczbę cykloootycznę hlporgrefu prostogo M przedstawionego no ryo.2.2. Hlpergraf ton aa dwie składowe spójności, tK(H) ■ 2, 10 wierzchołków x€X oraz 7 hiporkrawędzi.

Wartości k( u ) eę noetępujęcet k(Ej) - 2, k(Ej) ■ 2, k(E₃) • 2. k(E₄) -3. k(E₅) - 1. k(E₆) - 3. k(E_?) - 3. wobec tego

A(H) .SZfMuJ - ll ♦ 3£(M) - n(H) - 9 4 2 - 10 - 1 J-1 ^{L J    J}

Zouwożmy, żo w rozważanym hlpergraflo istnieje Jeden cykliczny łańcuch prosty (z dokładnośclę do wierzchołka początkowego i kierunku tworzonio cięgu okroólojęcogo ten łańcuch)

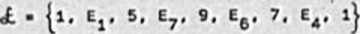
Przykład 7.2

Wyznaczymy liczbę cyklomotycznę grafu G przedstawionego na rys.2.3. Graf ten bo trzy składowe epójnoóci, 9 wlorzchoł -ków 1 16 gałęzi

A(G) •■♦iC-n«l6 43-9»10

Zauważey, żo w grafie tye istniejo dużo różnych prootych łań -cuchów cyklicznych.

Przykład 7.3

Wyznoczymy liczbę cyklomotycznę dowolnego dondrytu (on -tydondrytu). Kożdy dendryt (antydendryt) Jest grafów spójnym, 3C- 1, i Jeżeli posieda n wierzchołków, to z definicji me do-kłodnie m ■ n - 1 łuków. Zeteo

A»n-l4l-n-0

Zeuwożmy, żo dondryt (ontydendryt) nie zowlera łańcuchów cyk -licznych.

109