74646 P3200285

150

Wyznaczymy równania parametryczne płaszczyzny. Skoro Si jja₂. to weźmiemy pod uwagę wektory S\, PiPj (bo są nierównoległe). Zatem mamy

{z = 7 + 4* + 9s y = 2 — 6* — Aa , t. s £ R. z = —81 - 7s

GlO. Znaleźć dwusieczne kątów wyznaczonych przez proste przecinające się

x = 1 + 2* h- y = 2t

z = t

z = 11 + 8* lj : ■ y = 6 + 4* z = 2 + t

Naszkicujemy najpierw odpowiedni rysunek.

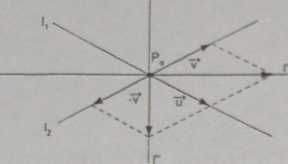
Wektory u, u są wektorami równoległymi do prostych odpowiednio Z_l5 /₂, przy czym |tt| = |u|.

Prosta V przechodzi przez punkt Po i jest równoległa do wektora u + v. Prosta l" przechodzi przez punkt Po i jest równoległa do wektora u — v.

• Wyznaczamy punkt przecięcia się prostych (tym samym sprawdzimy, czy proste l\, /₂ przecinają się).

z =1 + 2t_x    ( z = 11 + 8*₂

h ^; y = 2t\    /₂ :    y = 6 + 4*₂ (parametry oznaczone są inaczej)

z = 2 + *2

Porównujemy odpowiednie współrzędne.

2*i - 8*2 = 10

*i - 2*₂ = 3 *, - *2 = 2

1 + 2*_x = 11 + 8t₂ •    2*i = 6 + 4*₂ / : 2    =*-    •

*1 = 2 + i₂

oraz

+ 20 + 16 + 6 = -42 + 42 = 0 i -2

1 -1

Układ równań ma dokładnie jedno rozwiązanie, co oznacza, że istnieje jeden pnnkt wspólny obn prostych.

(Gdyby wcześniej zostało sprawdzone, że proste się przecinają, to od razu można byłoby przejść do rozwiązywania poniższego układu równań, gdyż skoro badany układ ma dokładnie jedno rozwiązanie, to wystarczy rozpatrywać tylko dwa równania.)

j U - 2t, = 3

| *11M I 2 - *2 = 1

tj =—1; ti = 2 + fj = 1

Parametr t\ = 1 wstawiamy do równań prostej (natomiast tj = —1 wstawiamy do równań prostej ł₂) i otrzymujemy współrzędne punktu Pq.

x— 1 + 2 = 3

*i = l

Rozwiążemy ostatni układ
-Capelliego.	2 -8
R{A) = R	1 -2	= 2,
	1 -1
	2 -8	10'
R(U) = R	1 -2	3
	1 -1	2

= 2, bo

bo

l -2 1 -1

= -1+2 = 1 =£0

2 -3 10

1    -2

1    -1

= -S - _-ł - 10+

V = 2    ; Po (3,2,1)

z = 1

Wyznaczamy wektory kierunkowe prostych l\, l₂ (z równań prostych).

Oi || *i, Oi = [2,2,1],    |oi| = \/4 + 4 + 1 = y/9 — 3

aj jj /j, a₂ = [8,4,1],    |a₂| = ^64+16+1 = >/8T = 9

Szukamy wektorów u, v, takich że u|| aj, w|| a₂ oraz |u| = |tJ|.

Np. S- 02 =[8,4,1], |«| = 9

u = 35i = [6,6,3], |u| = 3|ai| = 9.