006 3

Funkcja liniowa

PRZYKLAP:_

ł:y = -5x = 1

Czy A (O, 1) należy do prostej /?

Tak, bo po wstawieniu za .v = 0, za v = I otrzymujemy prawdziwe równanie 1 -—5-0+1 = 1

Czy 5(1,5) należy do prostej /?

Nic, bo po wstawieniu za .v = 1, r 5 otrzymujemy równanie 5=-l -5+ 1    5

ZADANIE 1__

Napisz wzór funkcji liniowej, której wykres jest równoległy do wykresu y = 2r + I i przechodzi przez punkt A{ 1, 5).

Rozwiązanie:

Trzeba napisać wzór funkcji liniowej, czyli innymi słowy wyznaczyćy = ax + b. Poszukujemy współczynnika kierunkowego u i wyrazu wolnego h.

.lak znaleźć a?

Szukana prosta jest równoległa do prostej y - 2x + 1. To oznacza, że obie te proste mają równe współczynniki kierunkowe. Stąd a = 2.

Mamy już c/, więc szukana prosta ma postać y = 2x + b.

Jak znaleźć b?

Wiemy, że prosta y = 2x + b przechodzi przez punkt .4(1, 5). To oznacza, że współrzędne tego punktu spełniają równanie tej prostej. A to oznacza, że po wstawieniu w miejsce .v= 1 i w miejsce r = 5 otrzymamy równanie: 5 = 2-1+/?. Inaczej 2 + b 5. Stąd wyznaczymy />; b- 5-2 = 3.

Szukana prosta ma postać y - 2x + 3.

Odpowiedź

y = 2v + 3

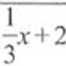
ZADANIE 2___

Napisz wzór funkcji liniowej, której wykres jest prostopadły do wykresu r = i przechodzi przez punkt B{-2, 1).

Rozwiązanie:

Należy napisać wzór funkcji liniowej y = ax + b. Poszukujemy współczynnika kierunkowego a i wyrazu wolnego b.

Jak znaleźć a?    I

Szukana prosta jest prostopadła doy ,.v + 2.

To oznacza, że współczynniki kierunkowe tych prostych spełniają równanie

-r*~''^e5)

a = 3

Szukana prosta ma postać y^: 3.v + b.

Jak znaleźć ó?

Wiemy, że prosta y = 3.v + b przechodzi przez punkt B(-2, 1). To oznacza, że po wstawieniu w miejsce x = 2 i w miejsce y I otrzymamy równanie prawdziwe 1=3- (-2) + b. Inaczej -6 + h I. Stąd h - 1.

Szukana prosta toy = 3.v + 7.

Odpowiedź

y= 3.v+7

ZADANIE 3___

Znajdź równanie prostej przechodzącej przez punkt A( 1, 5) i nachylonej do osi OX pod kątem a = 120°.

Rozwiązanie:

v ~ av + b, a - 120°

Wiemy, że tg u - a, zatem wstawiamy za a = 120* i obliczamy tę wartość, korzystając ze wzorów redukcyjnych.

a = tg 120° = tg (90° + 30°) = etg 30° = W!

a =

.V = -'JŚ.r + b oraz /l(l, -5) -5 = -V3 • 1 + b -5 + V3 = b

Mając obliczony współczynnik kierunkowy a wsławiamy go do równania prostej, a następnie obliczamy współczynnik b. Korzystamy z faktu, że funkcja przechodzi przez punkt A1. -5).

y = -V3.v - 5 + \'5

11