048(1)

(6, 2) i (6, 8). Obliczone wartości szczególne pochodnych są więc współczynnikami kątowymi stycznych do okręgu w tych punktach (rys. 37). 5) Pierwszy sposób. Różniczkując względem t, znajdujemy s'

1+i-²

S²+l

J²

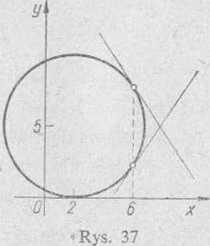
Ostatnią równość różniczkujemy ponownie względem r i wyznaczamy s '

2s’

s" = -2rV — s³

^Z.1 J

Zastępując teraz s' przez ostatecznie otrzymujemy

2(i^z+l)

⁴---

Drugi sposób, krotnie

Różniczkujemy daną równość względem t dwu-W+_T^- = 0    (a)

“^S+— (!+,=)=- =⁰ ®

Wyznaczając s' z równania (a) i podstawiając do równania (b), otrz>-mamy związek między t, s, s’\ z którego z kolei wyznaczamy s" jako funkcję t i s. Otrzymany wynik będzie taki sam, jak przy rozwiązaniu pierwszym sposobem.

6a) Różniczkując względem x, wyznaczamy y'

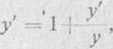
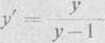
Ostatnią równość znów różniczkujemy względem i wyznaczamy y"

0-1)²

y'(y-\)-y'y

' “ O-O²

Podstawiając zamiast y znalezione wyżej wyrażenie, otrzymujemy

^y" ⁼ “ <y^W

6b) Daną równość różniczkujemy względem y i obliczamy x'

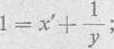
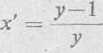
Otrzymaną rówmość różniczkujemy ponownie względem y; znajdujemy

,, _ l-y-Hy-l) _ y- f

Wyznaczyć pochodne funkcji uwikłanych:

227.    5x²+3xy—2y²-4-2 = 0; wyznaczyć y'

Ł L 1

228.    x³ +y³ = a¹; obliczyć y dla x = a

229.    e^sin* = e~^xcosy; wyznaczyć x'

230.    jfy =yx; wyznaczyćy

231.    x³+y³—3axy = 0; wyznaczyć y"

232.    y = tg(.v+y); wyznaczyć y"

233*. e^x—e^y = y—x‘, wyznaczyć y"

234.    x+y — e^x~^yi wyznaczyć y"

235.    y+r, In y = x-\-c₂\ wykazać, że yy" —(y')² l“ 00³ = 0

§ 10. Różniczkowanie funkcji danej równaniami parametrycznymi

Jeżeli funkcja y zmiennej niezależnej x jest dana równaniami parametrycznymi za pomocą zmiennej pomocniczej (parametru) t, czyli

*=/(0, y ~ vif)

to pochodne y względem x określone są wzorami

dy		dy'		dy"
dt	^d>' _	dt ,,,	_ _	dt
dx ’	dx	dx * ^	dx	dx
dt		dc		dt

(A)

7* 99