035 9

Ćwiczenie 4

Oblicz współczynnik kierunkowy stycznej do wykresu funkcji / w punkcie ,r₀. f(xo))- Podaj miarę kąta, jaki ta styczna tworzy z osią OX. f(x) = t², x₀ = 1 b) f(x) = x³, .T₀ = 2 c) f(x) = t₀ = 2

ZADANIA

1. Oblicz pochodne funkcji / w punktach tq i X\.

a) /(x) = 2, To = 3, Ti = 6

b) /(t) = 3t — 4, To = t, Ti = 5

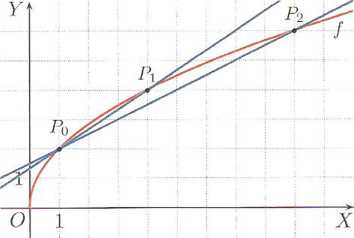
2.    Na rysunku obok przedstawiono wykres funkcji /(t) = 2a/t.

a)    Oblicz współczynniki kierunkowe siecznych Po Pi i P0P2 oraz wyznacz ich równania.

b)    Oblicz współczynnik kierunkowy stycznej do wykresu funkcji f poprowadzonej w punkcie Po.

3.    Oblicz miarę kąta, jaki z osią OX w punkcie (tq,/(to)).

a) /(t) = t², T₀ = -§ b) /(x)

c)    /(t) = 2t² — 1, to = — l,Ti = 2

d)    /(t) = T³, Tq = —2, Tj = 3

tworzy styczna do wykresu funkcji /

y, T₀ = 1 c) /(t) = y/x, t₀ = |

4. Przeczytaj podany w ramce przykład.

Przykład

Uzasadnij, że funkcja /(t) = \x\ nie ma pochodnej w punkcie xq = 0.

x I — 101    1.    x

- lim - = 1

a^o+ x

\ ^y
\l	/f
0	i i

/(ag)—/(O)

x—0

lim

:r—>0 *'    T 0

lim

lim

x—►O^-

x—0

0+ x—0 lim J2hM =

a—>0 *-0

lim — = -1

x^o^_ x

Oznacza to, że lim    /(°) _nj_c istnieje, czyli funkcja /(x) = |t| nie

x—*-0    X 0

ma pochodnej w punkcie Tq = 0 (chociaż jest ciągła w tym punkcie).

Uzasadnij, że funkcja / nic ma pochodnej w punkcie t₀.

a) /(t) = |t - 2|, To = 2    b) /(t) = t + |t|, t₀ = 0

5.8. Pochodna funkcji 287