033 7

Ćwiczenie 1

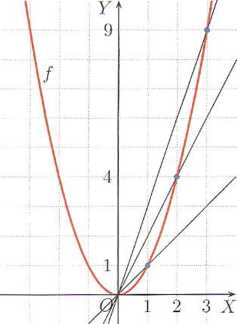
Oblicz współczynnik kierunkowy siecznej wykresu funkcji /(x) = x² (rysunek obok) przecinającej :en wykres w punkcie (0,0) oraz w punkcie o odciętej równej: a) 1, b) 2, c) 3.

Ćwiczenie 2

Naszkicuj wykres funkcji f{x) — — (x — l)² oraz sieczną wykresu przechodzącą przez punkty o odciętych .to = 1 i Ti = 2. Oblicz współczynnik kierunkowy tej siecznej.

Pochodna funkcji w punkcie

DEFINICJA____

Jeśli istnieje skończona granica lim ^^X1~Ł⁽'^XG'^>, to granicę tę nazywamy

X—>X()    ^{X X}°

pochodną funkcji / w punkcie To i oznaczamy f{xo):

/'(xo) = lirn f^-Kz-o)

^K ' X—±Xq X-Xq

Uwaga. Można wykazać, że jeśli funkcja ma w punkcie To pochodną, to jest w tym punkcie ciągła. Jednak z ciągłości funkcji w punkcie tq nie wynika istnienie pochodnej (patrz zad. 4).

Przykład 1

a) Oblicz pochodną funkcji /(x) = x² w punkcie to = 3.

lim (t + 3) = 6

x—^3

r(₃) = lim m-m = urn ^ = lim ^(x~³⁾⁽;⁺³⁾ =

^V    X~ 3    x — ó    X—>3    x — ó

b) Oblicz pochodną funkcji f(x) = T³ w punkcie tq = 2.

= lim

x—>2

x³—2³ x—2

/'(2) - lim

/(s)-/(2)

x—2

= lim(x² + 2t + 4) = 12 _<

x-+2

Ćwiczenie 3

Oblicz f(T₀).

a) /(t) = 5t — 3, t₀ = 1    c) f(x) = t³, to = — 1

b) /(x) = x² + 2, tq — 4    d) /(x) = x³ + 2, To = 3

5.8. Pochodna funkcji 285