img435 (2)

PRZYKIAD 14.

Zbadajmy istnienie asymptot pionowych wykresów funkcji:

x² - 6x + 8

x² - 3x + 2 x² - 4x + 3

a )/(*)=    *“¹

b )/(*) =

C)/M = x² + 2|x|

Ad a) Zauważmy najpierw, że D_f = (^o, 2) u (2, 4) u (4, +oo). Asymptoty pionowe mogą tutaj mieć równanie x = x₀, gdzie x₀ jest miejscem zerowym mianownika ułamka występującego we wzorze funkcji. Tylko w tych punktach bowiem granica może być niewłaściwa. Obliczamy więc odpowiednie granice jednostronne, wykorzystując wykres funkcji /(x) = x² - 6x + 8:

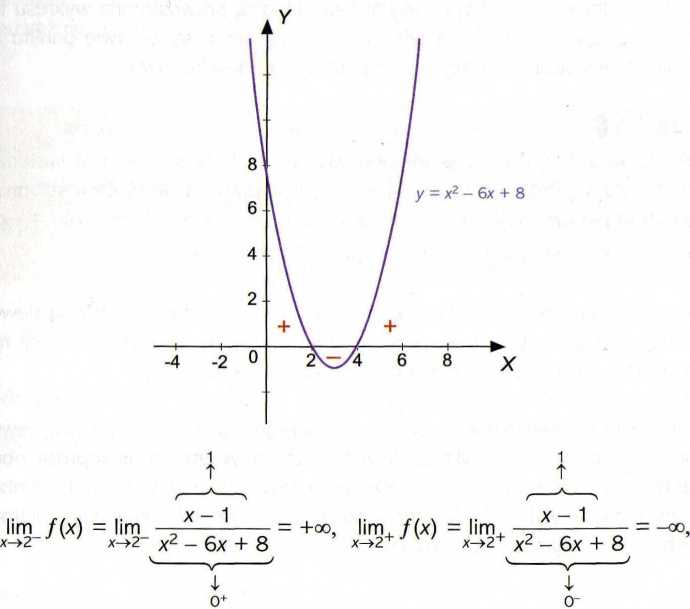
= -oo, lim. f(x) = lim,    *— -

lim l(x) = lim -    —--

• M    * >4" x² - 6x + 8

x->4+'^{/ v 7} x—>4⁺ x² - 6x + 8

■v

4

o⁺

Wobec ostatniej definicji wnioskujemy stąd, że proste x = 2 oraz x = 4 są

Myrti| (lotami pionowymi (obustronnymi) wykresu funkcji /(x) = Ad h) D_t = (-oo, 1) u (1, 3) u (3, +oo). Obliczamy:

x- 1

x² - 6x + 8

-1

t

(^x~ ^)(^x.    = |im AZA

x² - 3x + 2    ..

..... —- = lim —-—--—mu -

*-♦1 x² - 4x + 3 x->i (x - 1) (x - 3)    *-»¹ x - 3

lim

.

2

Analogicznie

lim

x² - 3x + 2    1

*—>¹⁺ x² - 4x + 3    2

Wnioskujemy stąd, że prosta x = 1 nie jest asymptotą pionową wykresu funkcji / (żadna z granic jednostronnych nie jest niewłaściwa).

Dniej obliczamy:

2

t

2

T

.. x² - 3x + 2 lim —-:-— = -00 ,

= +C0,

um_ —--

x->3 x² - 4x + 3

.. x² - 3x + 2 lim, —--

x-^3⁺ x² - 4x + 3

4

o⁺

4

Cr

(uzasadnij dokładnie te obliczenia!), skąd wnioskujemy, że prosta x = 3 jest asymptotą pionową wykresu tej funkcji.

Ad c) Stwierdzamy, że D_f = (-oo, O) u (O, +oo) (dlaczego?). Obliczamy granice jednostronne w punkcie x₀ = O:

o

T

o

t

lim_-= lim_

^x_>0 x² + 21 x |    ^x_>0

= lim

= lim

x² - 2x ^x_>0 x(x - 2)    ^x_>0 x - 2

4

o

4

-2

= 0,