052(1)

Współczynnik kątowy prostej w każdym jej punkcie ma jedną i tę samą wartość. Dla danej prostej wynosi on — J.

Zgodnie z wzorem (2), otrzymujemy

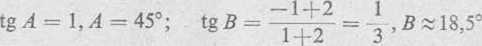
2) Rozwiązując układ równań obu krzywych, znajdujemy punkty wspól-

ne: A( 1,2, —0,8), 5(0, 1) i C(—1,2, —0,8); rys. 45. Następnie z równań

</

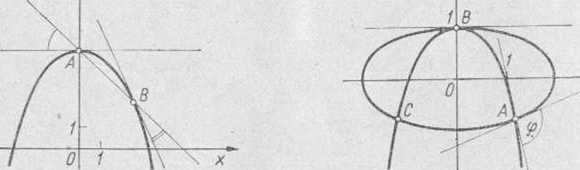
X

Rys. 44

Rys. 45

elipsy i paraboli wyznaczamy współczynniki kątowe dla dowolnego punktu każdej krzywej, jako pochodne y względem x

Podstawiając współrzędne punktu A otrzymamy

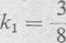
Wobec tego w punkcie A

8

W punkcie C krzywe przecinają się pod takim samym kątem, ze względu na symetrię obu krzywych względem osi Oy.

W punkcie B mamy ki = k₂ = 0, co oznacza, że w punkcie tym obie krzywe mają wspólną styczną i wobec tego nie przecinają się, lecz są tam wzajemnie styczne. Kąt między nimi w tym punkcie wynosi zero.

3) Odcięte punktów przecięcia się krzywych (rys. 46) są określone równaniem sinx = cos.v, które po rozwiązaniu daje

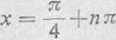
Za pomocą różniczkowania znajdujemy współczynniki kątowe stycznych do sinusoidy i cosinusoidy

k_x = cos*, k₂ = —sin*

Szukany kąt przecięcia się krzywych wyznaczamy z ogólnego wzoru (2)

cos *

tg?> = "jur

- sin *

cos xsm *

= ±

^y2- + 2 ⁺

1-

= ±2] 2

Dodatniej wartości odpowiada kąt ostry <p X 70,5°, a wartości ujemnej — kąt rozwarty, dopełniający do 180°; (pi = 180° — <p X 109,5°.

245. Dla danej krzywej x = t— 1, y =    wyznaczyć punkty,

w których styczna jest równoległa: 1) do osi Ox, 2) do prostej 9.*+y-r -3 =0.

Rozwiązanie. Proste są równoległe, jeżeli ich współczynniki kątowe są równe. Wykorzystamy ten warunek. W tym celu z równań krzywej znajdujemy pochodną y względem *

/ =    _₃e-12

' dt dt    1

która, jak wiemy, w dowolnym punkcie krzywej jest równa współczynnikowi kątowemu stycznej.

1) Przyrównując y do współczynnika kątowego osi Ox, równego zero, otrzymujemy

3z²—12 = 0, skąd t² = 4; t = ±2

107