091 3

Klnelyc/Jto-moIrkuUma teoria gazów. Prawa przemian gazów doskonałych

Podstawowe prawa gazowe wygodnie jest podać na podstawie rozważań kine-ryczno molekularnej teorii gazów*. Nie wchodząc w szczegóły tej teorii można stwierdzić. Ze gaz składa się z olbrzymiej ilości cząstek znajdujących się w sunie bezładnego mchu cieplnego. Cząsteczki te zderzają s»ę ze sobą. zmieniając swoją prędkość i kierunek ruchu Jeden mol dowolnego gazu zajmuje w warunkach normalnych objętość 22.4 • 10“* m* i zawiera około 6.02 - I0²’ cząstek gazu. Odległość międ/yc/ąsCec/kowa wynosi około 3 • 10“* m i jest o jeden rząd większa od odległości międzycząsteczkowych w cieczach i ciałach stałych (3 • IO‘^,0m). Jeżeli gaz. znajduje się w zbiorniku, to efektem olbrzymiej ilości zderzeń cząstek gazu ze ściankami zbiornika jest występowanie ciśnienia (p) wywieranego przez gaz na ściany zbsomika. Przyjmując, że zbiornik ma objętość (V). liczba cząstek gazu jest

m

równa (Aż), a —;— = £_k - jest średnią energią kinetyczną cząsteczki (gdzie C² jest

średnim kwadratem prędkości cząsteczki). Z teoni kinetycznej gazów wynika, że ciśnienie /> określa równanie:

P^m

l.£s

3 V

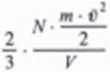
(6.28)

pdm £_% ■ N ■    ******* kinctycną wywlach c/atirc/rk ga/u w /bioanU

Gdy założymy, że ilość gazu w zbiorniku równa jest jednemu molowi, wtedy N m N_a m 6,02 • 10²* cząstek oraz

pV_m-RT    (6.29)

Równanie (6.29) nosi nazwę równania Clapeymna gazów- doskonałych. Porów nując powyższe równania oraz dokonując pewnych przekształceń, uzyskujemy związek pomiędzy średnią energią kinetyczną mchu postępowego cząsteczek a temperaturą bezwzględną T w postaci:

E_x = | • k T    (6.30)

ptx* k • I JM l(X²¹ 7    BotLmunru. %ul* Boiumaiuu k •    ; ftl/w R - tuto ga/im>

Ostatnie równanie (6.30) przedstawia kinetyczne okreHenie temperatury. które ma sens tylko w odniesieniu do wielkiej liczby cząsteczek gazu.

4

91