093 3

prostujące przeciwdziałające przechyłowi. Statek taki zachowuje się podobnie do statku o stateczności stałej. Jest jednak bardzo "miękki" i nawet mały moment powoduje powstanie przechyłu (GM = 0 na rys. 60).

Ramię prostujące statku o ujemnej początkowej wysokości metacentrycznej [32]

Jeżeli statek posiada ujemną początkową wysokość metacentryczną to znaczy GM < 0, wówczas równanie (4.5) ma dwa rozwiązania. Jedno gdy sin ę = 0 (<p = 0) jest stanem równowagi chwiejnej, a drugie:

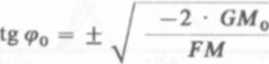
(4.13)

Wzór ten umożliwia określenie kąta przechyłu, przy którym statek uzyska ponownie równowagę. Statek taki w położeniu przechylonym znajduje się w stanic równowagi stałej, a jego wysokość metacentryczną określi zależność:

(4.13)

cos <p₀

Do wyprowadzenia wzoru (4.13) posłużyła zależność (4.5), której pochodna w kącie stałego przechyłu, po odpowiednich przekształceniach, dała ostateczne rozwiązanie. Przy stosowaniu wzoru (4.13) obowiązują zastrzeżenia określone przy wzorze (4.5).

4.6. Wpływ wymiarów kadłuba i położenia środka masy na przebieg krzywej ramion prostujących

Na przebieg krzywej ramion mają wpływ: szerokość statku, wolna burta i położenie środka masy statku. Rozpatrzony zostanie kolejno wpływ każdej z tych wielkości przy założeniu, że pozostałe nic ulegają zmianie. Przedstawione wykresy dotyczą barki prostopadłościcnncj, co nic zmienia jednak poprawności wyciągniętych wniosków [13].

Szerokość statku (rys. 62) ma duży wpływ na stateczność początkową i wielkość ramion prostujących. Zakres stateczności zmienia się nieznacznie z szerokością a wielkość ramienia prostującego przy kącie przechyłu 90° jest w rozpatrywanych przypadkach taka sama.

93