099 4

Zastosowanie modelu matematycznego wyższego rzędu lepiej odwzorowuje rzeczywiste zjawiska fizyczne w silniku Stirlinga, jednakże wyraźnie utrudnia wykorzystanie szeregu bardziej rozwiniętych i szybszych metod optymalizacji, np metod gradientowych. Obrazowy sposób dochodzenia do optimum funkcji celu różnymi metodami optymalizacji przedstawiono na rys. 3.19. W rezultacie prac przeprowadzonych przez zespół autora stwierdzono możliwość efektywnego wykorzystania bez-gradientowych metod poszukiwań prostych, lip. metody losowej lub Rosenbrocka oraz bezgradieritowych metod poprawy, np. Poweila lub Davisa-Swanna-Carnpeya. Oceniając zastosowane metody optymalizacji pod kątem czasu obliczeń prowadzących do znalezienia optimum funkcji celu, liczby wywołań funkcji celu, jak również wartości funkcji celu, w rozpatrywanym zadaniu najprzydatniejsza okazała się bezgradien-towa metoda Poweila z przesuwaną funkcją kary. Wniosek ten potwierdziły również prace innych autorów [121.

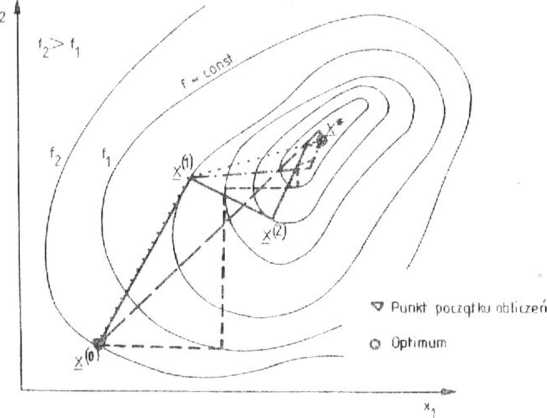
Rys. 3.19. Schemat dochodzenia do optimum funkcji celu różnymi metodami optymalizacji |6]

We wstępnym procesie optymalizacji należy określić możliwie wąski zbiór zmiennych decyzyjnych. Kiedy zbiór ten jest zbyt szeroki, proces optymalizacji wchodzi często w obszar poszukiwań z bardzo małą, lokalną wartością funkcji celu. Wynika to z faktu występowania w modelu matematycznym silnika Stirlinga licznej grupy rozwiązań z określonym ekstremum lokalnym.

Wybranie wąskiego zbioru zmiennych decyzyjnych odbywa się drogą ich selekcji pod względem rodzaju wymiennika ciepła, np. dla chłodnicy, nagrzewnicy lub regeneratora. Po znalezieniu przybliżonych wartości optymalizowanych zmiennych możliwe staje się przystąpienie do łącznej optymalizacji wszystkich zmiennych decyzyjnych .

103