100719

MATERIAŁY rX2YMERSKIE

dxni3 (przy tych samych obci42cmach). Ponadto jeden z nich    ^

niższa granicę plastyczności i może ulegać odkształceniu pJ^ZUjCznac5ne Potrzebna jest więc analiza podobna do przeprowadzonej w rozdz^^^

TABLICA 27 3

Moduł Granica

Stal miękka

Slai wysokowytrzymała

Stopy aiomimum

OFRP (kompost polimerom wzmacniany krótkim włóknem szklanym )

Gęstość	Younga	plastyczności	płE'°
> Mg-nT*	E GPa	/?. MHa	N^,V-^,<w
7.8	207	220	nr
7.8	207	do 500	1.32
2,7	69	193	0,66
1.8	15	75	0.73

N'Vy

0.53 0.35 0.19 0.21

Materiał*

Jtewe. Matom »    «>«*«!

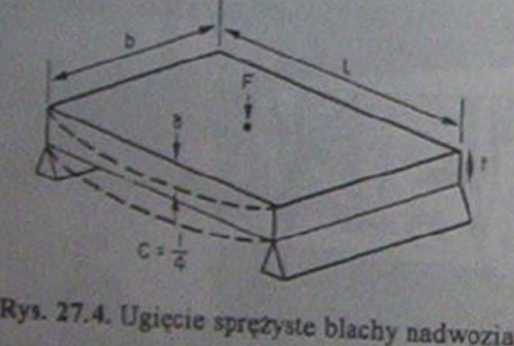
Mleż. jako aUcrr^s^^i ?^'’ nadwozia) ważne jest spręż, sic ujrn *« Ile, sic    “ Podobnej sztywność, J,

padku zderzaka). nalczs DoróMtn- ^*^saałccnic plastyczne (jak np w p ^^“aałcenie plastyczne lieiecie^snr ^^rZckrojc ° jednakowej odpornośu ■>5 -^{7 4}) jest dane wzorem P^rc^>^e o'blachy pod działaniem -

M    _d=£l±

Ebt*

k_ra S^,oko“ ^{su,a c c}

⁰³ wybbt niateriaJa Masę btaeh^lcra

w = pbtl

2*9

aielkośc b i / ™l konstrukcj. pojazdu (rozmiaru drzwa >*p ) ^{Jcdyną zin,cnną}-^{0(1 którc}J say^noić

(27 1) otrzymujemy    *">• -I⁶⁵¹ 1

i =

W"

l<5£6_y

(27 3)

Po podstawieniu tego wyrażenia do równania (27.2) otrzymujemy wzór określa-masę blachy

, , , .

M -

Cl ~ż \l^fb²

P_

\E'ⁿ

(27.4)

Ze wzoru tego wynika, że przy danej sztywności (FIS) oraz danych wymiarach i podparciu (/, b, C) blachy, jej masa jest najmniejsza dla najmniejszej wartości plE"

Podobne rozumowanie można przeprowadzić dla odkształcenia plastycznego Blacha o przekroju pokazanym na rys 27.5 ulega płynięciu przy obciążeniu

Cbt

R.

(27 5)

F =

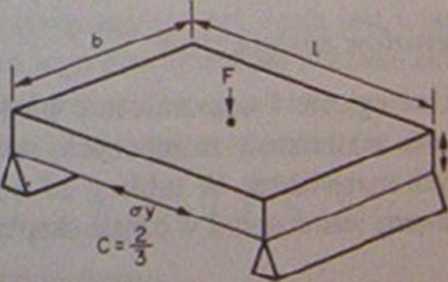
Ryt. 27.5. Odkształcenie plastyczne blachy nadwan*

Podobnie jak poprzednio, masę blachy obliczamy zc wzoru

(27.6)

M = pbtl

^Wzorzc tym występuje tylko jedna zmienna r, którą obliczam, kształcenia wzoru (27.5)

r

^ł FI l CbR,