0172

173

§ 1. Pochodna i jej obliczanie

Przy tych samych oznaczeniach, co i wyżej, otrzymujemy

u+Au

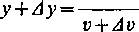
a więc

Au-v — u-Av

v(v + Av)

Au    Av

— • v — u • — Ay Ax    Ax

Ax    v(v + Av)

Przechodząc do granicy przy Ax dążącym do zera (przy czym jednocześnie i Av~¹0) przekonujemy się, że istnieje pochodna

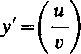
u v — uv

98. Pochodna funkcji złożonej. Możemy teraz wyprowadzić bardzo ważną dla praktycznego obliczania pochodnych regułę pozwalającą obliczyć pochodną funkcji złożonej, jeśli znane są pochodne funkcji składowych.

V. Niech 1) funkcja u— tp(x) ma w pewnym punkcie x₀ pochodną u'_x = <p'(x₀), 2) funkcja y=f(u) ma w odpowiednim-punkcie u₀ = ę(x₀) pochodną y'_u=f'{u₀). Wtedy funkcja złożona y—f{<p(xj) ma również w wymienionym punkcie pochodną, równą iloczynowi pochodnych funkcji f (u) i tp(x):

[f(<p(x)j]' =fu((p(x₀))ę'(x₀) O,

albo krócej:

Dla dowodu nadajmy x dowolny przyrost Ax; niech Au będzie odpowiednim przyrostem funkcji «= ę{x), a Ay — przyrostem funkcji y—f{u) odpowiadającym przyrostowi Au. Skorzystajmy ze wzoru (2a), który napiszemy zmieniając x na u w postaci

Ay = y'_uAu + aAu

(a zależy od Au i dąży razem z Au do zera). Dzieląc każdą stronę tej równości przez Ax otrzymamy

1

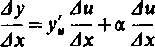
Podkreślamy, że symbol fi(ę(xj) oznacza pochodną funkcji /(u) względem jej argumentu u (a nie względem x) dla wartości u= <p(x) tego argumentu.