0176

177

§ 1. Pochodna i jej obliczanie

1    Jax + b — yjb — ac

19) v---ln^ -—~—    (zakładamy, że b — ac>0) ;

yjb—ac yj ax+b+yj b—ac

21) y=

1

y/a^T²'

asmx + b

arc sin-

a + b sin a:

1

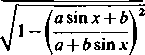
(|*| <a ; -in<x<in) ;

acosx-(a+6sinx)—(asinx+ł>)- bcos* (a+b sin x)²

1

a+bsinjc ‘

1    b+asiax-Jb²-a²cosx

22) y= -_r^=r ln- ■, ,    _:- (W<|b|);

yj b² — a²

a+bsinx

1 /	a a 2 yjax+b 2 y/ax+b	1
1 •o > 1 \	_y/ax+b—yj b — ac yj ax + b+ yj b — ac_	(x+c)yjax+b
2	1 ax + b
-arc tg yj ac—b	. / - (tu zakłada się, żc ac—b> 0) ; V ac — b
2	1 1 a	1

sjac — b ^ . ox+b yj_ac—b 2yjax+b (x+c)yjax + b ac — b

1 r acosx+yJb²—a² ńnx    bcosjc "|    1

V*²

~a² Lb+asinx—-y/b² — a²cosx a+bsinxj a+bsinx

23) Rozpatrzmy jeszcze jako ćwiczenie obliczenie pochodnej wyrażenia potęgowo-wykładniczego y=u“ («> 0), gdzie u i o są funkcjami x mającymi w danym punkcie pochodne v\

Logarytmując równość y=u^v otrzymamy

(5)

\ny=vlnu,

Wyrażenie na y można więc napisać w postaci y=e^v"“, skąd rzecz jasna wynika, że pochodna y' istnieje. Samo obliczenie jej można najprościej wykonać, przyrównując pochodne względem x obu stron równości (5). Wykorzystujemy przy tym reguły V i III (pamiętając o tym, że u, v i y są funkcjami x). Otrzymamy

1 . 1

— • y'=v'\nu+v • — u’,

y    «

skąd

/W ,    \

y =y I—■+v'\nu\,

albo, podstawiając zamiast y jego wyrażenie,

(6)

+a'ln«|.

Wzór ten był po raz pierwszy wyprowadzony przez Leibniza oraz Jana Bernoulliego. Na przykład, jeśli

y=x"°* , to y'*=x‘^lax ^^+cosjclnxj.

12 G. M. Fichtcnholz