0157

ROZDZIAŁ III

POCHODNE I RÓŻNICZKI

§ 1. Pochodna i jej obliczanie

90. Zadanie obliczenia prędkości poruszającego się punktu. Zaczniemy od przykładu szczególnego, rozpatrzymy mianowicie spadający swobodnie (w próżni — aby nie uwzględniać oporu powietrza) ciężki punkt materialny.

Jeśli czas t (sek) będziemy liczyli od początku spadania, to droga s (m) przebyta w ciągu tego czasu wyrazi się, na mocy znanego wzoru, następująco:    (j

(1)    s = $gt²,    J

•Mt

Rys. 36

gdzie 3 = 9,81 m/sek². Wychodząc z tego, trzeba określić prędkość u punktu w danej chwili /, gdy punkt znajduje się w położeniu M (rys. 36).

s + As — ^g{t+At) , As = }g(2tAt+At²).

Nadajmy zmiennej t pewien przyrost At i rozpatrzmy chwilę t+At, gdy punkt będzie w położeniu M_x. Przyrost MM_y drogi odpowiadający okresowi czasu At oznaczmy przez As. Podstawiając do wzoru (1) t+At zamiast t otrzymamy wyrażenie

skąd

Dzieląc As przez At otrzymamy prędkość średnią spadającego punktu na odcinku MM_X

śt

As

At

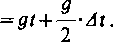
v

Jak widzimy, prędkość ta zmienia się wraz ze zmianą At, stan spadającego punktu w chwili t jest opisany tym lepiej, im mniejszy jest okres At, który upłynął od tej chwili.

Prędkością v punktu w chwili t nazywamy granicę, do której dąży prędkość średnia v_iT odpowiadająca okresowi At, gdy At dąży do 0.

W naszym przypadku jest oczywiście

v= lim {gt + \gAt) = gt. ai->o