0180

181

§ 1. Pochodna i jej obliczanie

101. Pochodue nieskończone. Jeśli stosunek przyrostów Ay/Ax przy Ax~*0 dąży do + oo (—oo), to tę liczbę niewłaściwą nazywamy również pochodną i oznaczamy jak zwykle. Analogicznie wprowadzamy pojęcie pochodnej nieskończonej jednostronnej. Geometryczna interpretacja pochodnej jako współczynnika kątowego stycznej pozostaje w mocy i w tym przypadku, lecz tutaj styczna jest równoległa do osi y (rys. 43a, b, c, d).

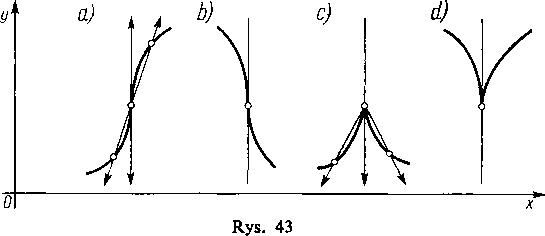
W wypadkach (a) i (b) pochodna ta równa się odpowiednio + oo i — oo (obydwie pochodne jednostronne mają te same znaki); w wypadkach (c) i (d) pochodne jednostronne mają różne znaki.

Niech na przykład będzie fi(x)=x^i/3; ze wzoru 3, ustępu 95 otrzymujemy dla x?0:

;

wzoru tego jednak nie można zastosować dla x=0. W punkcie tym obliczymy pochodną wychodząc bezpośrednio z definicji. Tworząc stosunek

f₁(0+Ax)-f₁(0)_(Ax)^i/l    1

Ax    Ax Ax²'³

możemy zauważyć, że granica jego przy Ax-*0 będzie równa +oo. W podobny sposób możemy się przekonać, że dla funkcji f₂(x)=x²^³ w punkcie x=0 pochodna lewostronna równa się — oo, a prawostronna + 0O.

Korzystając z uogólnionego pojęcia pochodnej można uzupełnić twierdzenie z ustępu 94 o pochodnej funkcji odwrotnej uwagą, że i w tych wypadkach, gdy f'(x₀) równa się 0 lub ±oo, pochodna funkcji odwrotnej g’(y₀) istnieje i równa się odpowiednio ±oo lub 0.

Na przykład funkcja sin jc ma dla x= +%n pochodną cos (±^n)=0, dla funkcji odwrotnej arc sin y istnieje zatem w punkcie y= ± 1 pochodna nieskończona (mianowicie + oo).

102. Dalsze przykłady przypadków specjalnych. 1° Przykłady nieistnienia pochodnej. Już funkcja y= |jc| nie ma w punkcie x=0 [100] zwykłej, dwustronnej pochodnej. Ciekawszy jest jednak przykład funkcji

/(*)=.* sin — (przyx#0), /(0)=0, x