0178

179

§ 1. Pochodna i jej obliczanie

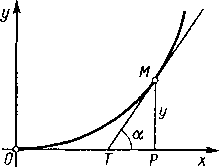
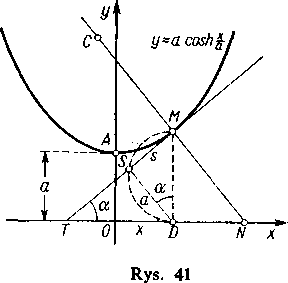
tak więc y cos a=a. Jeśli z podstawy D rzędnej y=DM (rys. 41) opuścimy prostopadłą DS do stycznej MT, to odcinek DS okaże się równy a.

Stąd wynika znowu prosty sposób konstrukcji stycznej do rozpatrywanej krzywej: na rzędnej DM jako na średnicy budujemy półokrąg i z punktu D zataczamy luk o promieniu a do przecięcia się z pól* okręgiem w punkcie S; prosta MS będzie właśnie styczną.

29)    Niech punkt materialny drga wzdłuż osi wokół pewnego środka według prawa

sin (to/+a)    (A,a>> 0).

Drgania takie noszą nazwę harmonicznych; A nazywa się amplitudą, w — częstością, a — fazą początkową. Obliczając pochodną drogi s względem czasu t znajdziemy prędkość ruchu

v—Aoi cos (cot—a).

Największą wartość ±Am osiąga prędkość, gdy s=0, tj. gdy punkt przechodzi przez środek. Na odwrót, gdy punkt znąjduje się w największej odległości od środka (s= ±A), prędkość c=0. Pochodna v względem t:

a— — Aa? sin(tu/+a)

jest przyśpieszeniem punktu; oczywiście

a= —oj² • s.

Stąd, jeśli wprowadzić masę m punktu ruchomego, to zgodnie z prawem Newtona siła F, pod której działaniem odbywają się drgania harmoniczne, wyrazi się wzorem

F— — mco²s.

Widzimy, że jest ona skierowana zawsze ku środkowi (gdyż ma znak przeciwny do znaku s) i jest proporcjonalna do odległości punktu od środka.

30)    Ruch odbywający się według prawa

s=Ae~^k,s'mcot (A,k,co> 0)

nazywa się ruchem harmonicznym tłumionym, obecność bowiem czynnika e~^k‘ zmusza punkt, by drgając wprawdzie wokół położenia środkowego, dążył jednak do zetknięcia się z nim

lim 5=0.

t-> + CO

12*