0174

175

§ 1. Pochodna i jej obliczanie

x sin*+cos*

5) y=---—. Tu trzeba skorzystać najpierw z reguły IV, a potem z reguł II i 111 i ze wzo-

x cos*—sin*

rów 6, 7 [95]:

(x sin*+cos*)'(* cos*—sin*)—(* sin *+cos*)(* cos*—sin*)'

/= ---:-:—Ti--

(* cos*—sm*)

* cos*(* cos*—sin*)—(* sin*+cos*)(—* sin*)    *²

(* cos*—sin*)²    (* cos*—sin*)² ’

Obliczanie pochodnych licznika i mianownika wykonaliśmy nie rozbijając rachunku na oddzielne kroki. Należy w ogóle dojść przez ćwiczenia do takiej wprawy, by pisać pochodne od razu.

Przykłady obliczenia pochodnych funkcji złożonych:

6)    Niech y = lnsin*, innymi słowy, y=lnu, gdzie « = sin*. Według reguły V, y'_x—y'_u-u'_x. Pochodna y'„=(ln u)'_u-=— (wzór 5) powinna być obliczona w punkcie «=sin *. W ten sposób

u

1    cos*

y_x—--(sin*)' —-=ctg* (wzór 6).

sm *    sin *

7)    y=Vl +*², tj. y=\/«. gdzie u= 1 +*²; według reguły V jest

1 ₂ *

^ń==-rifT^'^{(1+x y=}~ir1=i <^wzór <³>; przykład 1).

2yJl+X    V I +JC

8)    y=e^xl, tj. y=e“, gdzie « = *²;

yi=c*V)'=2*/    (V;4i 3).

Oczywiście można nie wypisywać oddzielnie funkcji składowych.

9) y=sin ax\ y'„ = cos ax (ax)' = a cos ax (V; 7, 1, 2).

10)    y=(*²+*+l)"; yi=n(*²+*+l)"^_1(*²+*+l)'=n(2*+l)(*² + *+l)^,,_1 (V; 3 przykład 1).

11)    y = 2“^nx; y'_x = 2’¹”* In 2 (sin *)' = ln 2 cos * 2*¹"* (V; 4, 6).

1

12) y=arctg—;

*

yi=

l

ił?

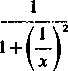
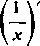
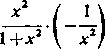
(V ; 12, 3).

Przypadek funkcji złożonej, otrzymanej w rezultacie kilku superpozycji, sprowadza się do kilkakrotnego zastosowania reguły V.

13) j>=Vtgi*; tutaj jest

y’x=-j -:-(tgł*)i= (V ; 3)

²Vtgi*

(V; 8)

²yjtgi* COS² i*

1

4 COS² ixj^_x