0164

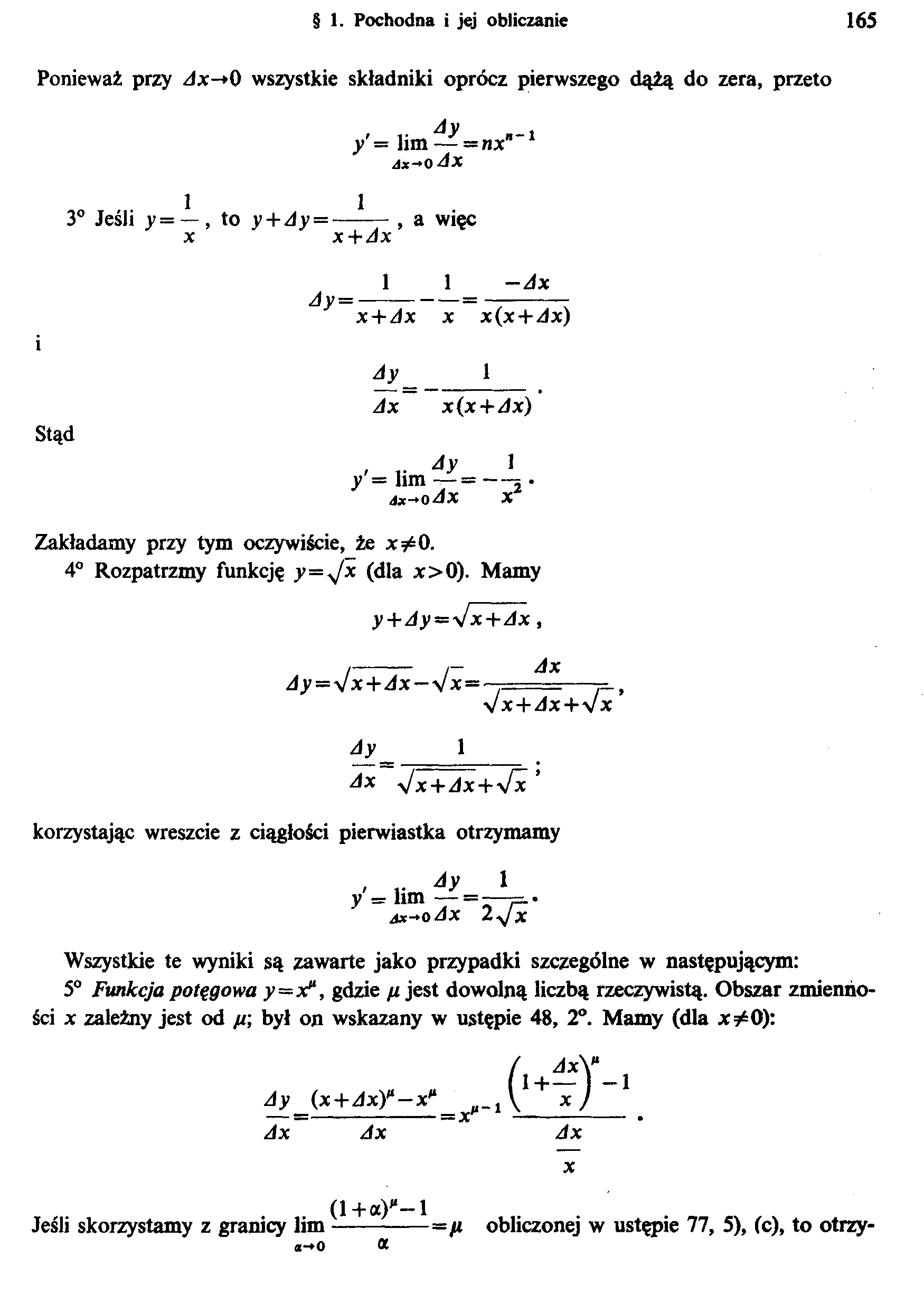
165

§ 1. Pochodna i jej obliczanie

Ponieważ przy Ax~*0 wszystkie składniki oprócz pierwszego dążą do zera, przeto

Ay , /= lim — = nx jx—o Ax

3° Jeśli y= — , to y+Ay=—-— , a więc x    x+Ax

Ay=

1

1

—Ax

x + Ax x x(x+dx)

Ay    1

Ax x(x+Ax)

Stąd

, _v Ay ¹ J’ = lim —=

dx-*Q*X

Zakładamy przy tym oczywiście, że x#0.

4° Rozpatrzmy funkcję y=*Jx (dla x>0). Mamy

y + Ay = y/x+Ax,

Ay = \lx+Ax—yJx—

Ax

yJx+Ax+\Jx ’

Ay

Ax yjx + Ax + \fx

korzystając wreszcie z ciągłości pierwiastka otrzymamy

' ^Ay 1 y — lim —=-—=.•

JX-*0 Ax 2yjX

Wszystkie te wyniki są zawarte jako przypadki szczególne w następującym:

5° Funkcja potęgowa y=x'\ gdzie p jest dowolną liczbą rzeczywistą. Obszar zmienności x zależny jest od p; był on wskazany w ustępie 48, 2°. Mamy (dla x#0):

Ay (x+AxY — x^l‘

Ax

Ax

= x

Ax

x

(l_+a)<*_l

Jeśli skorzystamy z granicy lim-—p obliczonej w ustępie 77, 5), (c), to otrzy-

«-*0 ot