10687535w0293806352126232805868418956254 o

iui| (p

I ■»

U»| (a

310. Wykami. żc lezą twierdzenia Uprany a mc jest pnwOaw dla następujących funkcji:

a) f(x) = —    w przedziale (-ki):

3.39. Wykazać. ż* wykresy ^runkc)’

„ » *>

,_lBl.    d) p(«)-tf^^+b-

C) Hj) t* -i\TM ,

_są wypukłe (ku górze) w przedziałach okreMonoic.

. . .    _____linii

I

yi Z _* «1 DJ«    .o* *

_;_t_«n «ł '(o<<?)    •-—- “*^,ł <*

ni M

I

c)    M*)-'¹'

d)

-

b) p(.t) = I -    w przedziale (-1.2)

311 Napisać wzór I.agranpe a dla podanych ntzet funkcji i obliczyć c

są wypukłe (ku górze) w pr/*u--------

_M„. _Wym.* ^.tr -W"'™”“°“

W \ v* 3r-2'    b) *(^x)⁼ _ri _J'

a) /(*) = * ^3v '    *

2Ti,* ,_q

jit uis|u|

ł-

armia j8 ?<zat|qo Ot r 8p

ru(

uii| (8

a)	A*)=*‘	» przedmie	(°- *)
b)	g(x) = x’	w- przedziale	("•*)
c)	A(x)=^x{	w przedziale	(14):
d)	f(x) = arctgx	w przedziale	(0.1):
e)	C(x) = arc sin r	w przedmie	(0.1):
0	H(x) = In r	w przedziale	(U 2).

c) h(x) = x'e'\

1

c) «(jt) = (^Jt_1V'¹'

341. Wyznaczyć punkty przegięcia krzywych.

(x-l)’

^d)

x 3i .

' x£ 3)

uit| 0

I- -Z

;i_± uii| O

r+,z

(,a-,

•'*    ’ Uli) (p

(o-l)ui

((r-iluisU i—

• l'    '—!— un\ (a

_a) Ą_x) _{= x}'+3x'-9x-2; b) S(')= _x,

-— uit| (q

i*

x u|

uit) (®

■

■

dla dowolnego

dla dowolnego i

361. Napisać wzór Maclaunna dla

a)    /(x) * xe’    dis

b)    g(x) = srn’ x    dl

c)    h(x)' yl*’+*■ ’) d

d)    p(*) = tg x    dla n = i

^e> *(*) = arc sin x dla n =

362 Obliczyć przybliżoną wartość lunl a) /(x) = cos.r;

^c)

III 1

312. W jakim punkcie styczna do linii i = 4-r^: jesl równoległa do cięciwy łączącej punkty .<(-2.0). «(U)? Wykonać odpowiedni rysunek.

313. Wykazać. żc podane w tym zadaniu funkcje są funkcjami pierwotnymi tej samej funkcji:

a)    /(x)=lnox    i

b)    A(x)=2sin^Jx    i

c)    ż"(x) = (e' +e")    i

g(x)=lnx;

p{x)=-cos2x;

C(z) =

314. Wykazać, żc funkcja:

a)    /(.r) = cos²x + cos' y-m ,-cosxcosfy*xj;

b)    g(x)=2arctgx-arcstn—(zil);

l + z

d, p(.r)=_fl-^;

o KO=^,e~''

h) u(z) = e‘ cos z. z e (0.2rt)

_ IŻL _ma trzy punkty przegięcia leżące na jedne,

342.    Wykazać, żc krzywa y - ^ _{+ J}

^Pr0S,CJ'    ,    ; h punk, (1.3) jest punktem przeg.ęcia krzywe,

343.    Dla jakich wartości u P

y = tf.t* + b.X‘ •

c) /i(.v) = ln(l ^{+ ;t} )^;

c) g(x) = xlnx;

:*>tuŁCi ?Xzoitqo 9fi

g) 4')

(t^+,)^U| —

■ . ^VJ-L- IUII (q

x St 3JE Z - u

x 3t x ,®~*

•-:— uin (3

xi\-x

dla x = 0.01 i n 2 . Oszacować I 363. Oszacować błędy bezwzględne

a, sin***- — x’

6

V = OX + DX ■

^y    nrzcdzialy wypukłości i wklęsłości wy-

344. Wyznaczyć punkty przegtęca oraz. przedz, ,P

kresów funkcji-

a?0;

jest stała.

b) g(x) = -»⁴(^121nx"⁷'^-

c) /i(x) = arc tg r-arc sin-r== Vx^J +1

-V-

• ,^A..'

⁴,\$n

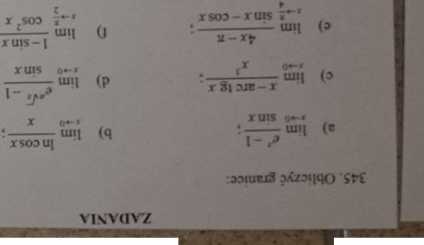
364 Obliczyć przybliżoną wartość fun a, /(x) = sinx;

b) Igisz + yr’

,    a⁵ X¹ x‘

c) e *l + x+ — + — + — 2!    3!    48

d, VTT7« 1+-- — 2 8

w

dis

dla

dla

dla

.

* -    '•    • * •*    t    ^ i A -• '    *•

|v

Al *    -jf ¹    • "*. ■