111(1)

Ostatnią całkę h znajdujemy osobno, wg reguły podanej w § 5. nownik sprowadzamy do postaci kanonicznej: 4 —x + l = (x—~ 3    I

-f ■ ₄- i podstawiamy x - ₇ t. Mamy wówczas dx = di oraz

Mia-

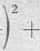
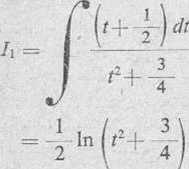
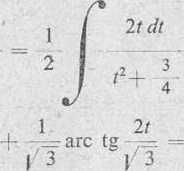
di

+

1    , . ,    1    2x- 1

= ~In(x²—x+l)4--— arc tg - -

²    i 3    | 3

Podstawiając ten wynik do poprzedniej równości, otrzymamy |x| (4- x- 1)    2    2.v — 1

. '-‘-„w -r3^arcl83 j^+c

4) Rozkładamy ułamek pod całką na ułamki proste:

a)    .4 4 łOjr-j-25 = (x*+5)²

4 — 3    Ax \ B Cx+D

^b)    (4+5)² “ .4-i-5 ⁺ (4+5)²

c)    4-3 = (AxVB) (44-5)4-Cx+D -

= Ax^l+Bx² -f (54+ C)x+ (5B - D)

B = 0,	54+C		= 0. 5B+D = -3
B = 0, C		-5,	D = —3, czyli
	4	-3	x 5x4-3
	(x^2-	|-5)^2	^- x^2+5 (x^2+5)^2
4 — 3		r	x dx e f x dx
(4+5)^2		J	4+5 ^5J (44-5)^2

Całkujemy Pierwszą całkę sprowadzamy do wzoru 2

dx

T4+5)²

f x dx 1	C 2 xdx 1	■4(44-5) 1
' x^2 + 5 2 J	x^24-5 2 J	4+5 2

■

Drugą sprowadzamy do wzoru 1 xdx 1

2(x²+5)

W trzeciej całce dokonujemy zamiany zmiennej, podstawiając x = |/5 tgz. Wtedy dx = ] 5 sec² z dz, a więc

cos² zdz —

r dx _ r { 5 sec² zdz _ 1 r

J Jx²+5)² ~ J 25 sec⁴ z ~ 5 j/5 J '

=    -7= I (1+cos 2z) ć/z =——r=/z-f—7-sin 2z\ =

10J/5J    lOj/5 \    2    )

1

10|/5

Ostatecznie otrzymamy 1

=    ■7= jare tg W +

* | 5

JO

x²+-5

^I=Ą- ln(V--5) + y-f—--(arc tg ~    ^ ) + C =

2    2(x^z-j-5)    10j 5 l j 5    **+5/

-	2 ^ln(x 5)+ l0(x^2+5) '	Wy'5	arc tg —— -j- C V^5
Obliczyć całki :
527.	[• dx	528.	f dx
	J ^-jc^2		J *^3+x
529.	r xdx	530.	f (x^2+l)dx
	J x^3-\		J x^3—3x^2+3x— 1
531.	• (7x— 15) r/.v j x^>-2x^2-j-5x	532.	r 2t^s-2t+i J - 1-f *
533.	f z^2dz	534.	r x^4dx
	J z^4+5z^2+4		J x^4-2.x^2+l
535*.	r (x+l)dx J x^4+4x^2+4	536*.	r !-*• , J r+*< *

§ 8. Całkowanie niektórych funkcji niewymiernych

Całki funkcyj niewymiernych (a także przestępnych) wyrażają się przez funkcje elementarne tylko w pewnych określonych przypadkach. Do najczęściej spotykanych typów całek funkcyj niewymiernych, wyrażających się przez funkcje elementarne należą następujące całki.

15 Metody rozwiązywania zadań 225