119(1)

■

1.    Rozkładamy u na dużą liczbę « małych elementów składowych Au,-

n

u = A tł{ -f-żl U2~\~... ~\~A u_n ⁼ ^ ^ A Ui

i^i

2.    Znajdujemy przybliżoną wartość każdego elementu Au_t w postaci iloczynu Au, ~ f(x ) • Ax, a następnie przybliżoną wartość u w postaci sumy całkowej

n

MS',^\f(Xi)Ax    (*)

gdzie:

x —jeden zparametrów wielkości u, który na podstawie warunków zadania przebiega wartości ze znanego przedziału a < x < b\

f(x) — dana lub określona przez warunki zadania funkcja x;

Xo — a,xi,X2,...,x_n — b — punkty przedziału [a, ó], które przy rozłożeniu wielkości u na n elementów dzielą ten przedział na n równych części Ax = = (b-a)!n.

Przy znajdowaniu przybliżonej wartości małego elementu . 1 u-, czynione są różne założenia. Zakłada się np., że małe odcinki zakrzywionych łuków wolno zastąpić przez cięciwy łączące ich końce, że siłę zmienną (lub prędkość) wolno zastąpić przez stałą siłę (lub prędkość), przyjmując, że dany wektor zachowuje na całym, małym elemencie drogi tę samą wielkość i ten sam kierunek, jakie miał w początkowym lub końcowym punkcie tego elementu drogi. Analogicznie zakładamy, że zmienną w czasie temperaturę ogrzewanego lub studzonego ciała wolno w małych odstępach czasu uważać za stałą, tj. przyjąć, że w ciągu każdego małego odstępu czasu temperatura zachowuje tę samą wartość, jaką ma na początku lub przy końcu danego odstępu czasu.

3.    Jeśli z warunków zadania wynika, że dla n -* -j-oo błąd przybliżonej równości (*) dąży do zera, to poszukiwana wielkość u będzie co do wartości

b

liczbowej równa całce oznaczonej u = J f(x)dx.

a

Wiele wielkości można wyrazić za pomocą całki oznaczonej posługując się innym schematem (II):

1.    Zakładamy, że pewna część u(x) obliczanej wielkości U jest niewiadomą funkcją, przy czym x jest jednym z parametrów wielkości U i przebiega znany z warunków zadania przedział wartości a < x < b.

2.    Znajdujemy różniczkę du funkcji u(x), czyli przybliżoną wartość (część główną) jej przyrostu Au, gdy x zmienia się o małą wielkość dx, w postaci iloczynu du = f(x)dx, gdzie f(x) jest daną lub określaną przez warunki zadania funkcją .v.

Także i tutaj czynione są różne założenia, sprowadzające się na ogół do tego, że przy zmianie argumentu x o małą wielkość dx przyjmuje się, iż zmiana u(x) jest proporcjonalna do dx.

3. Stwierdziwszy, że różniczka du “została wyznaczona poprawnie, czyli że dla dx -» 0 obie-wielkości nieskończenie małe Au i du są równoważne", wielkość szukaną U znajdujemy przez scal Iłowanie du w granicach od x = a do x = b

b

U = J f(x)dx

a

Pole dowolnej figury płaskiej w układzie współrzędnych prostokątnych można utworzyć z pól trapezów krzywoliniowych, przylegających do osi Ox lub do osi Gy.

a) Dla trapezu krzywoliniowego, przylegającego do osi Ox (rys. 93), różniczką zmienne;, o pola S(x) — S_XlA!l{x jest pole prostokąta o bokach y i dx, czyli dS — ydx

Pole S_Xl4Bxj, w przypadku gdy cały trapez leży nad osią x, wyraża się przez całkę

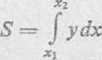
0)

b) Dla trapezu krzywoliniowego przylegającego do osi Oy (rys. 94), różniczką zn lennego pola S(y) = S_ytAu_y jest pole prostokąta o bokach X i dy, czyli 4l' — xdy.

a

y

Rys. 93

Rys. 94

0 Gdy dx -> 0 granica stosunku-powinna być równa jedności albo różnica

du

Au—du powinna być wielkością nieskończenie małą rzędu wyższego niż Au i du.

241

16 Metody rozwiązywania zadań