130(1)

2)    Stosujemy wzór (I), przy czym przekształcamy go, przechodząc na podstawie równań asteroidy do zmiennej t. Otrzymamy

71

T _

5 = 2 • 2tz I y \ x²-\-y^z dt =

6

71

*2___

= 4rc f asin³t\/(~3acos²tsint)²+(3asin²tcostydt = ó

IL    ⁷¹

T    Y

= 12a²n I sin⁴icos/<* = 12a²7t f sin^tdsint —

o    b

Jl

— ~ a²7t [sin⁵/]^ = -g-

(Czwartą część asteroidy, leżącą w pierwszej ćwiartce (rys. 112), otrzymujemy, gdy t zmienia się od 0 do rr/2).

3)    Równanie elipsy różniczkujemy obustronnie względem x; mamy

“2x %yy^ł    t    b²x^

~^T    -^r — °> skąd yy' = — —p . Na podstawie wzoru(l), otrzymujemy

a    a

S = 2tv f y |/l+O')² dx = 4tt J y'y²+(yy')² dx =

-a    0

•    . f, /,₂    ó²*² ó⁴x²    4rró f /    a²- b² ,

-Hy*¹—5T+-S*-*-—J j/-²- -?■ *■&=

4.TÓ

a

?—(²x² dx

a ■ ya²—b² c .

gdzie s =-= - — mimośrod elipsy.

aa

Podstawiając = nsinf, otrzymamy edfc = acostdt oraz: = 0, gdy x = 0, ti = arc sin e, gdy x — a, czyli

12

4rró C

12

„ 4wó f r-5-. ₇ a , 4nab f . ,

S =- l/a²—a²sin²f    costdt =---- cos ²tdt =

a J    e    s J

2?c ab

f

i i *

j (l-j-cos2t)dt = —

2 nab

e

f+y sin2r

= 2 nb (b-j- — arc sin e.

\ ^£

Gdy £-»0, otrzymujemy wzór na pole powierzchni kuli 5 = 4rrer.

655. Obliczyć pole powierzchni, utworzonej przez obrót wokół osi Oy : 1) luku okręgu i-(j' ~W~ — R² między punktami, w których y — y, i y = y₂, 2) pętli krzywej 9ax² = j(3a—y)¹.

Rozwiązanie: 1) Jeśli luk danego okręgu nie przecina osi Oy (czyli w fasnej średnicy), to przy jego obrocie wokół tej osi powstaje powierzchnia, którą nazywamy dwukątem sferycznym (rys. 121). Różniczkując

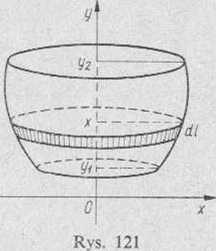
obustronnie równanie okręgu względem y, mamy 2xx’ -r2(y—b) = 0, skąd = — (y—b) Na podstawie wzoru (2) otrzymujemy

Z2    >2

S — 2tz j x\/\ \-(x'fdy = 2n jj \x²+(xx‘)ⁱdy =

>'i    yi

>2

= 2ti J ) R^z— (y—b)²+(y—b)²dy =

)[2

— 2nR I dy = 2nR{y₁—y_l) = 2nRH

yi

gdzie H oznacza wysokość dwukąta sferycznego. Gdy H = 2R, otrzymujemy dobrze znany wzór na pole powierzchni kuli S = 4rrR².

263