133(1)

661. Jaką pracę należy wykonać, aby wypompować zc zbiornika pionowego (walec o wysokości H = 6 m i o promieniu podstawy R = 2 m) zawarty w nim olej o ciężarze właściwym <5 — 0.9 G/cm\

Rozwiązanie. Praca L wykonywana przy podnoszeniu ciała zależy od wysokości x, na jaką podnosimy dane ciało, czyli L — Gx, gdzie G — ciężar ciała.

Załóżmy, żc praca zużyta na wypompowanie ze zbiornika warstwy oleju o grubości a: (rys. 126) jest pewną funkcją L(x) i znajdźmy różniczkę tej funkcji.

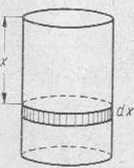
Rys. 126

' Jeżeli x zmieni się o wielkość c!x, to objętość V warstwy oleju zmieni się oAV — nR¹dx, jej ciężar zmieni się o AG = JtdR¹dx, a praca wykonywana zmieni się o AL ~ nóRr • xdx = dL.

Całkowitą pracę L otrzymamy, gdy a: zmieni się od 0 do H, a więc

H 1 xdx — 7t 6 R^2	'.X^1" o
0

H

0

ndR¹H¹

___<"V»*

2

64 800rr kGm ~ 64 800 • 9,81» J«63S688wJ^ł>

662. Obliczyć pracę, jaką trzeba wykonać, aby wypompować olej ze zbiornika cylindrycznego opisanego w poprzednim zadaniu, lecz o osi symetrii skierowanej poziomo.

Rozwiązanie. Zakładamy, tak samo jak przy rozwiązywaniu poprzedniego zadania, że praca zużyta na wypompowanie ze zbiornika warstwy oleju o grubości x (rys. 127) jest pewną funkcją L(x) i znajdujemy różniczkę tej funkcji.

Jeżeli :c wzrośnie o dx, to objętość V warstwy oleju wzrośnie o - Hydx = dV, jej cięż.ar .G wzrośnie o wielkość AG Z Hvd dx = dG, a zużyta praca L powiększy się o AL a: dHyxdx = dL.

Całkowita praca Z, wyrazi się całką z dL, w granicach od * = 0 do x = 2R

2R    2 R

L — 6H J xydx = 2<3H J x \^/R²—(x — R)² dx o    o

przy czym zmienna y została wyrażona w funkcji zmiennej x z trójkąta prostokątnego ONM.

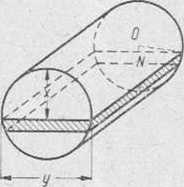
Rys. 127

Aby obliczyć tę całkę podstawiamy x—R ^ Rsint, skąd dx = Rcostdt oraz: t = —— dla x — 0 i * = y dla x = R. Mamy więc

~2

L = 2óH ) (R+R sin t)R² cos² tdt —

Jt

~2

2Ó//R? [ j cos²tdt+ j cos²r sin tdt\² „ =

* .1    71

= 2 ÓHR³

1    1    -T²

— sin2t—— cos³r    =

4    3    _J_n_

= ndHR² = 43 200rr kGm ss 423 792-r J

663. Na dnie basenu o głębokości H = 14 dcm znajduje się kula. Obliczyć, jaką pracę trzeba wykonać, aby wydobyć tę kulę z wody, jeżeli promień kuli R = 3 dcm, a jej ciężar właściwy <5 = 2 kG/dcm³.

269

1

ss 0,102 kGm, 1 kGms 9,81 J.

2

) J (dżul)—jednostka pracy w międzynarodowym układzie jednostek SI; 1