144(1)

697.

697.

dx

i (4“^p

698. f ^xd.-L J x’-l

699.    Oblicze pole zawarte pomiędzy krzywą y — e ³ i osiami układu współrzędnych (dla x ^ 0).

l/e*

700.    Obliczyć objętość bryły powstałej przez obrót krzywej v =

(dla x > 0) wokół jej asymptoty.

§ 11. Całkowanie przybliżone

• Istnieje kilka sposobów przybliżonego całkowania. Jeżeli funkcja f(x) dana jest albo za pomocą pewnego wzoru, albo za pomocą tablic jej war-

h

tości, to całkę oznaczoną /f(x)clx możemy obliczyć w sposób przybliżony następująco:

1)    dzielimy przedział całkowania [#, b\ na n równych części h = --°~

za pomocą punktów x_ł; x₂, x₃,..., x„_,,

2)    obliczamy wartości funkcjj podcałkowej y = f(x) w punktach podziału, czyli obliczamy y₀ = f(a), y_: =/(x,)_; y„_, = /(x„_,), y„ = f(b),

3)    posługujemy się którymkolwiek ze wzorów całkowania przybliżonego. Najczęściej stosowane są następujące przybliżone wzory, oparte na geometrycznym przedstawieniu całki oznaczonej jako pola trapezu krzywoliniowego.

I. Wzór prostokątów

b    n — i

(la)

j ydx v h{y_<i+y_x'-y₁+ ... +y„_,) =h ^ y,-

/«=0

albo

J ydx ss A(yi+y₂+y₃+ - +y_n) = h y_{

(Ib)

1=1

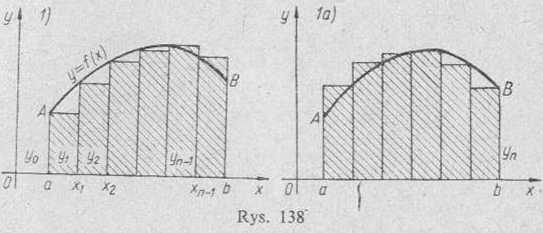
Geometrycznie (rys. 138) wzór ten oznacza zastąpienie pola trapezu

b

krzywoliniowego aABb, odpowiadającego całce f ydx, sumą pól prosto-

a

kątów, zakreskowanych na rysunku.

Błąd powstały przy przybliżonym obliczaniu całki oznaczonej w'g wzoru prostokątów ma oszacowanie

k<    ^Q)² »

<H«) < —y_nw

gdzie y'„oznacza najw iększą z w artości |/| w przedziale [a, b].

II. Wzór trapezów

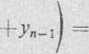
J ydxxh^^y°^- ...

(2)

Geometrycznie (rys. 139) wzór ten oznacza zastąpienie pola trapezu Krzywoliniowego sumą pól trapezów', zakrcskowanych na rysunku.

Błąd we wzorze trapezów ma oszacowanie

<5(«)

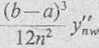
gdzie y„_w — największa z wartości |y"\ w przedziale [a, b\.

III. Wzór trapezów parabolicznych (czyli wzór Simpsona)-, u jest tu liczbą parzystą.

♦ b

•» ^

J ^ydx~ ^    fj..-f-40,+d’3+ - t-J_n-i)-f2ly₂+j₄+ ... +.y_n_₂)] (3)

a

Geometrycznie (rys. 140) na podstawie tego wzoru pole każdej pary pasków ^x‘^pi^pi i*i~2 jest zastępowane polem trapezu parabolicznego (oznaczo-

19*

3 291