175(1)

Posługując się wzorami (2), obliczamy najpierw m_x i m_y, a następnie masę m trójkąta (ze wzoru (1))

ABC    0    y-a

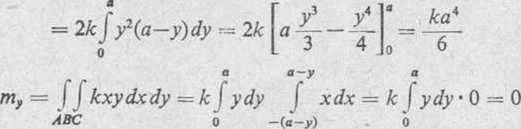
a a—y    a

ABC    0    y—a    0

Rys. 175

m = J f kyd\dy = k Jydy | dx = 2k J y(a—y)dy — —^

a nr    n    ..    3

W rezultacie x_c = — = 0, y_c = — = —.

m    m 2

Gdyby w całym obszarze trójkąta rozkład masy był jednorodny, środek ciężkości wypadłby w punkcie przecięcia środkowych boków, czyli w pun-

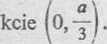
834. Dla trójkąta opisanego w poprzednim zadaniu obliczyć moment bezwładności względem przeciwprostokątnej.

Rozwiązanie. W przyjętym w poprzednim zadaniu układzie współrzędnych mamy obliczyć moment I_x. Korzystamy z pierwszego ze wzorów (3)

a    a-y

^w    “ y    “    e

T_x = ff ky³dxdy = k f y³dy J dx = 2kj y³(a—y)dy = —

ABC    0    y—a    o

835. Płytka jednorodna jest ograniczona dwiema elipsami współśrod-kowymi o pokrywających się osiach (pierścień eliptyczny). Obliczyć momenty bezwładności płytki względem jej osi symetrii.

Rozwiązanie. Jeżeli osie układu prostokątnego pokrywają się z osiami symetrii pierścienia, a półosiami zewnętrznej elipsy są ci i b\, zaś wewnętrznej ai i bi, to równania tych elips będą miały postać

Szukanymi momentami będą wtedy I_x i /„. Stosując wzory (3) oraz uwzględniając symetrię płytki (D) względem osi współrzędnych, otrzymamy

D

I_x = J j yr6dxdy = 4ó[J f fdxdy— J j y²dxdyj

gdzie Dj i D_z — obszary leżące w pierwszej ćwiartce płaszczyzny, ograniczone odpowiednio zewnętrzną i wewnętrzną elipsą.

Całkujemy najpierw względem y, a potem względem x

0^ 0 0 0 0 0

Aby obliczyć te całki stosujemy podstawienie: w pierwszej całce x = fljsin/, a w drugiej x = fl₂sin t

2

TC

T

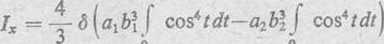
o    o

2

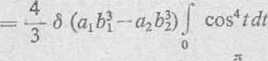
0

Jak obliczyliśmy w zad. 512 (2); całka j _ccs*tdt = —

I_x = ~7ib(a_yb\—a₂bl)

Analogicznie, stosując drugi ze wzorów (3), znajdziemy

--7ió (b_la\—b₂cĄ)

353