HWScan00124

4.6. Wyznaczanie optimum kształtu przekroju skiby

Przy posługiwaniu się metodą obliczania mocy w odniesieniu do liniowych jednostkowych oporów kopania wprowadzono stosunek = m^zy

określający kształt skiby w przekroju poprowadzonym na wysokości osi koła. W celu uzyskania minimum mocy kopania konieczne jest ustalenie optimum współczynnika m w zależności od kąta urabiania ę?_u [163].

4.6.1. Równanie funkcjonalnej zmiany grubości skiby w przebiegu skrawania

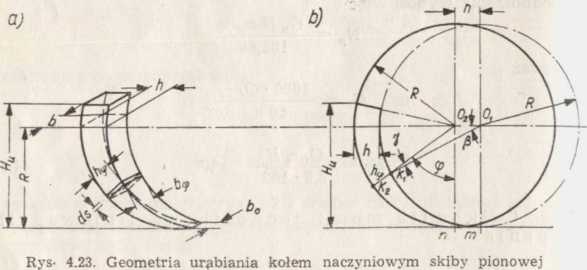
Dla określenia równania grubości skiby h, = f (<p) można napisać dla dowolnego położenia naczynia K> (rys. 4.23) odpowiednio do trójkąta ostrego 0,0₂K, wg prawa sinusów

0i0₂ =__0,K,

sin y sin (90 + <p)

albo

0,0,    0,K,

sin y cos cp

Zgodnie z rys. 4.23 po podstawieniu 0,0-2 = h oraz 0,K, = R, określimy, że

sin y = -n cos cp    (4.62)

łi

Dla tego trójkąta można napisać

0₂Ki ₌ OiKi sin P cos (f

ponieważ odpowiednio do rys. 4.23 0->K, = R — h,_t , więc

R — h_v R

obwiązując względem h otrzymamy

h* = R - R    (4.63)

Kąt P w trójkącie O1O0K1 określają zależności

P = 180 —(y + 90    <p) = 90 — y — q>

sin P = sin (90 — y — q>) = cos (y + 9?)

_n I    sin y sm 9? \    ...

R I cos y —----- (4.64)

\    '    cos (p /

podstawiając wartość sin P w równanie (4.63) po przekształceniach otrzymamy

ha = R

COS- <p

Wykorzystując równanie (4.62) otrzymamy cos y

Podstawiając cos y i sin y do równania (4.64) otrzymamy wyrażenie h_v = R — /R² ~~ h² cos²<p + h sin 9?

Po przekształceniach wyrażamy zmienność wielkości h_v równaniem

K = h    cos ² 9? i- sin <p j

Oznaczając stosunek obu stałych geometrycznych wielkości przez

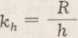
(4.65)

otrzymamy    ‘

h₇. = h(k_h — /kh~ cos²9? + sin (p)    (4.66)

Ponieważ wartości k_h 1 i cos\ < 1, to zawsze słuszna jest zależność

kn > cos²9?

Jest to warunek szeregu binomicznego o dodatnim wykładniku (a ± x)^m. Można zatem dla uproszczenia zależności

— cos²ę? = (k*_h ~ cos²9o )²

napisać

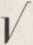
. ,    „    . cos ²99    2 cos⁴9?    3 cos V

k_h — cos-9? k_h 2 k_h ~    8k*    48 k⁵h

Od trzeciego wyrazu wartości rozkładu są tak małe, że bez większego błędu można je pominąć. W ten sposób grubość skiby pobieranej przez naczynie obrócone o kąt 93 określamy wyrażeniem

K = h | sin (p 4- -7^- cos²ę? j

m

(4.67)