177 3

a) b)

f)

00 01

^xl^x2

*\	00	01	^11	10	y
(00)- 1	O	O	^5	4	0
(ID- 3	-	4	©	4	i
(10)- 4	1	(i)	©	0	0
(OD- 5	-	-	3	-	-

A'

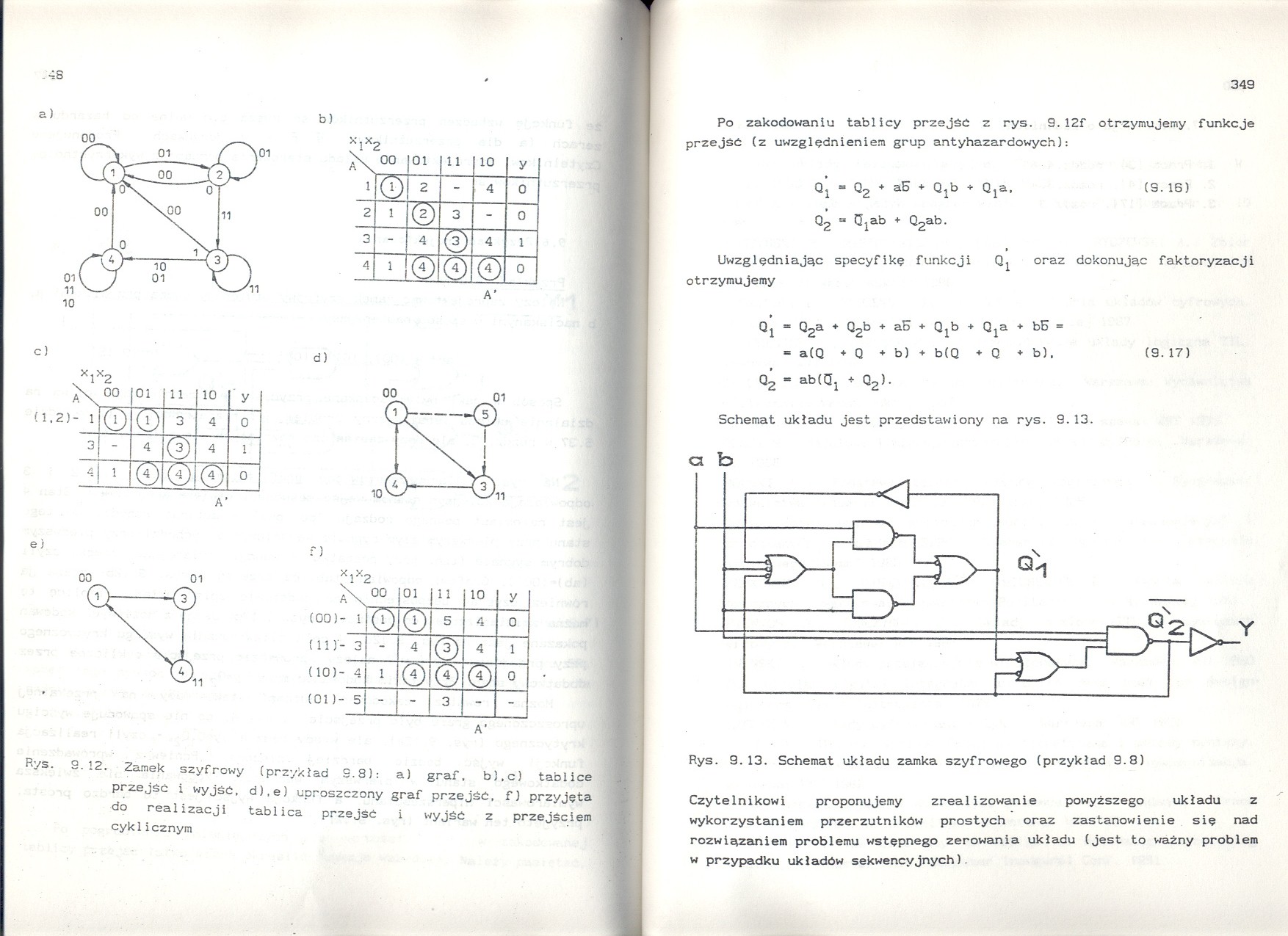
Ryś. 9.12. Zamek szyfrowy (przykład 9.8): a) graf. b).c) tablice przejść i wyjść, d),e) uproszczony graf przejść, f) przyjęta do realizacji tablica przejść i wyjść z przejściem cyklicznym

Po zakodowaniu tablicy przejść z rys. 9.12f otrzymujemy funkcje przejść (z uwzględnieniem grup antyhazardowych):

(L = Q₂ + a5 + Q,b + Q^a,    (9.16)

Q₂ = Qjab + Q₂ab.

Uwzględniając specyfikę funkcji    oraz dokonując faktoryzacji

otrzymujemy

Ql = Q₂a + Q₂b + a5 + Qjb + Qja + b5 =

= a(Q + Q + b) + b(Q + Q + b).    (9.17)

Q₂ = ablCJj + Q₂).

Schemat układu jest przedstawiony na rys. 9.13.

a fci

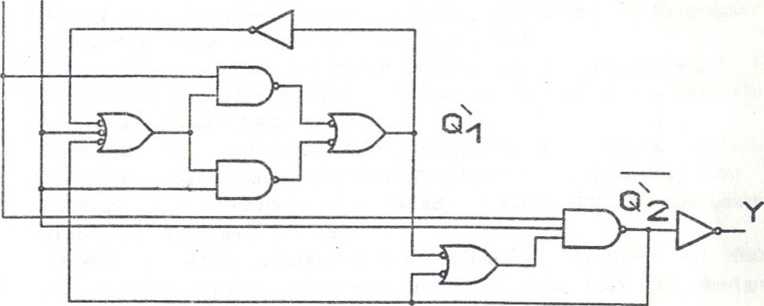
Rys. 9.13. Schemat układu zamka szyfrowego (przykład 9.8)

Czytelnikowi proponujemy zrealizowanie powyższego układu z wykorzystaniem przerzutników prostych oraz zastanowienie się nad rozwiązaniem problemu wstępnego zerowania układu (jest to ważny problem w przypadku układów sekwencyjnych).