pkc15

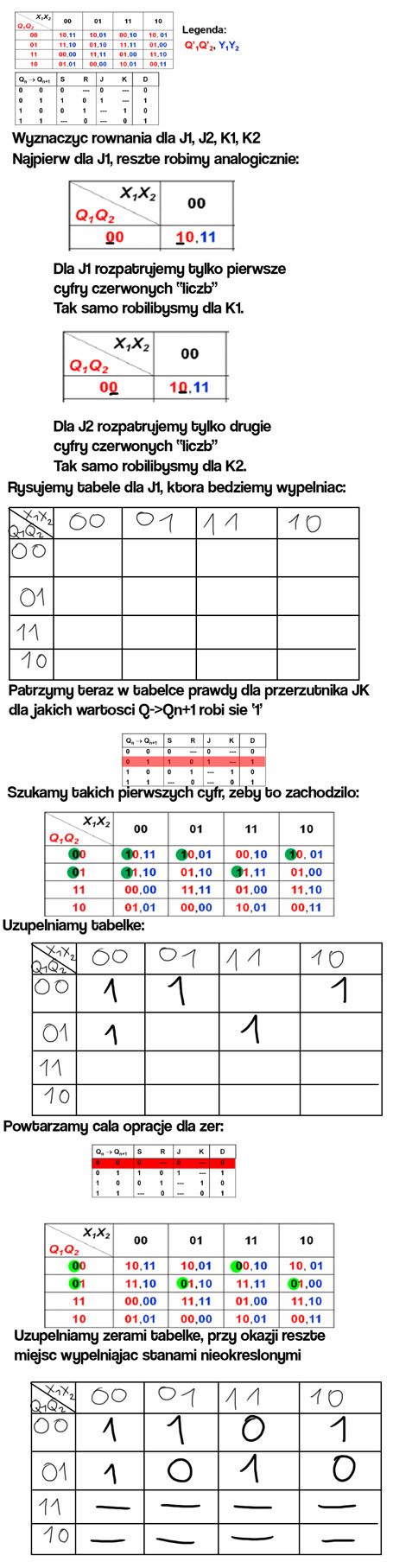
xtxi 0.0,	00	01	11	10
oo	10.11	10.01	00 10	10.01
01	11.10	01.10	11.11	01.00
11	00 oo	11,11	01 00	11.10
10	01.01	00.00	10.01	00.11

Legenda:

Q\Q'₂, y,y₂

©„-►o,.,	S R	J K	D
0 0	o	0 -	0
0 1	1 0	1 —	1
1 0	0 1	— 1	0
1 1	- 0	— 0	1

Wyznaczyć równania dla J1, J2, K1, K2 Najpierw dla J1, reszbe robimy analogicznie:

x,x2 q1q2	00
Q0	10.11

Dla J1 rozpatrujemy bylko pierwsze cyfry czerwonych "liczb”

Tak samo robilibyśmy dla K1.

*1*2 Q,c?2	00
oa	10.11

Dla J2 rozpatrujemy tylko drugie cyfry czerwonych "liczb”

Tak samo robilibyśmy dla K2.

Rysujemy tabele dla J1, która będziemy wypełniać:

>Q„., |

S R JJ    K

o    “‘o    —~

mm

D

0

F- ?

M t !

Szukamy takich pierwszych cyfr, zęby to zachodziło:

SSn	Oo	01	/M	10
OO
01
11
10

Patrzymy teraz w tabelce prawdy dla przerzubnika JK dla jakich wartości Q->Qn+1 robi sie T

XiX2 0,0?	00	01	11	10
®0	•0.11	•0.01	00.10	•o. 01
	#1.10	01,10	•1.11	01,00
11	00.00	11.11	01.00	11.10
10	01.01	00.00	10.01	00.11

Uzupe niamy babelke:

	oo	01	/M	10
oo	A	1		1
01	A		1
11
10

Powtarzamy cala opracje dla zen

|o.	>0~,	1^s	R |j	K	^0 i
0	1	1	^0 1^1	•M	1
1	0	0	1 —	1	0
1	1	1 —	o l —	0	1

XiX2 0,02	00	01	11	10
soo	10.11	10.01	•0.10	10. 01
#1	11.10	•1.10	11.11	01.00
11	00.00	11.11	01.00	11.10
10	01.01	00,00	10,01	00,11

Uzupełniamy zerami babelke, przy okazji reszbe miejsc wypełniając stanami nieokreślonymi

2$	O O		A A	10
OO	A		0	1
01	A	o		0
11	-—	—		■--
10	—	—	•—'	—