178(1)

w którym G_xy jest rzutem obszaru G na płaszczyznę xOy, a z — y',(a, y) i z = rpł(x_xy) są równaniami powierzchni ograniczających obszar G od dołu i od góry.

Wzóf ten sprowadza obliczenie całki potrójnej do kolejnego obliczenia zwykłej (jednokrotnej) całki oznaczonej względem zmiennej z, przy czym zmienne a-, y traktuje się wtedy jako stałe, i całki podwójnej o zmiennych całkowania x i y, rozpostartej na obszar G_xy leżący w płaszczyźnie xOy.

Z reguły granice całki wewnętrznej (jednokrotnej) są zmienne. Zależą one od tych dwóch zmiennych, które przy obliczaniu tej całki są traktowane jako stałe. Granice obydwu całek będą stale tylko wtedy, gdy obszarem całkowania jest walec prosty, o tworzących równoległych do osi Oz i podstawach leżących na płaszczyznach równoległych do płaszczyzny xOy.

Zamieniając role zmiennych a, y i z we wzorze (*), można otrzymać inne analogiczne wzory na obliczanie całki potrójnej za pomocą kolejnego obliczania całki zwykłej i całki podwójnej.

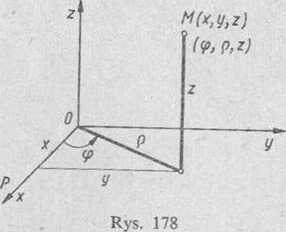
Przy obliczaniu całki potrójnej w podany wyżej sposób, niekiedy, po obliczeniu całki wewnętrznej, warto przed obliczeniem całki podwójnej wprowadzić współrzędne biegunowe, jak to objaśniamy w § 2. O tym' sposobie obliczania całki potrójnej mówimy, że polega on na sprowadzeniu całki do współrzędnych walcowych, gdyż jak widać z rys. 178, zmienne <p, Q i z są właśnie współrzędnymi walcowymi punktu M(x, y, z)

Całkę potrójną można też obliczać inaczej: najpierw obliczyć całkę podwójną, o zmiennym obszarze całkowania, a potem całkę jednokrotną.

1 1 2

849. Obliczyć całkę trzykrotnie iterowaną /= f dx f dy f (4j-z)dz

-i x* o

i określić, co przedstawia obszar całkowania.

Rozwiązanie. Obliczamy kolejno trzy zwykłe (jednokrotne)

całki oznaczone, zaczynając od całki wewnętrznej

7, = /<4+z)<fe = [^]’ =    = 10

1 1

h = Jlidy = 10 /</y = 10[y]‘_s = 10(1 -,v²)

X2    X2

11 , h = /= J /₂<& =10 | (1 -.vV-V = ¹⁰ X - - J- = -y-

Teraz, podobnie jak przy obliczaniu całki podwójnej, można się posłużyć

bardziej zwartym zapisem

ii    ₂    .ii    i

/= | dx I —k£— dy — 10 | dx f dy = 10 j (1 —x²)dx —

— 1 Ara

—    -*⁰    -i    -i

Aby przedstawić obszar całkowania danej całki, należy najpierw napisać równania ograniczających go powierzchni. Przyrównując każdą ze zmien

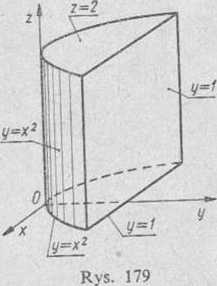
nych całkowania do granic odpowiadającej jej całki, otrzymamy następujące równania

* = — 1, x = 1, y = x², y — 1, z = 0, z — 2 Konstruując w układzie współrzędnych Oxyz te powierzchnie (rys. 179), widzimy, że ograniczają one prosty walec, o tworzących równoległych do

osi Oz.

359