180(1)

2) Obszar W ograniczony dana powierzchnią jest elipsoidą obrotową (rys. 183). Rzut W_xy obszaru na płaszczyznę xOy jest kołem a^-24-y²    a².

Stosując wzór (*), otrzymamy

r = r_c

J= f fdxdy f (x²Ą-y²+z²)dz

' *4

gdzie r_v i z_Q — wartości z obliczone z równania elipsoidy:

^zn,<2 = TV3(a²-x²-y²).

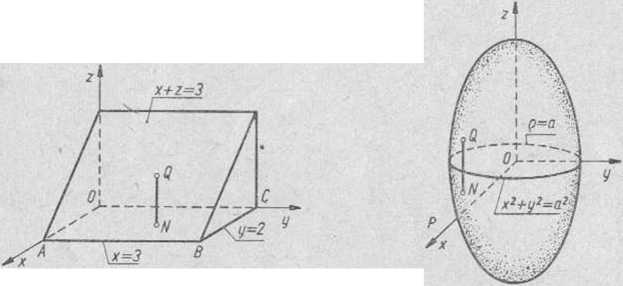
Rys. 182    Rys. 183

Obliczamy całkę wewnętrzną (całkę jednokrotną względem z)

J= f I (x*+y*)z+y

K

dxdy = 2a² j 3 j' j \a² — x²—y²dxdy ~^N    x²+y²ka²

Z kolei, aby uprościć obliczenie otrzymanej całki podwójnej sprowadzamy ją do współrzędnych biegunowych. Podstawiając x = geosęr, y = gsimp i zastępując dxdy przez ody do, otrzymamy

7«=2a²]3    a²—q² gdpdg =

C<a

2ji 0    i

= a²}^3 j d<p | (a² — Q²)²d(a² — Q²) =

0    a

Ana*

W

(równanie okręgu a²T^² = a² w tych współrzędnych ma postać q = a).

3) Dane powierzchnie ograniczają stożek T, przedstawiony na rys. 184. Każda prosta, przechodząca przez punkt wewnętrzny stożka równolegle do osi Oy, przecina jego granicę tylko w dwóch punktach, a rzut l_xz stożka na płaszczyznę xOz jest kołem x^ljrz¹ < h². Biorąc to pod uw^fagę,

przekształcamy wzór (*), zamieniając rolami zmienne z i y. Otrzymamy wówczas

____

K—JJ dxdz f ycly, gdzie: y_s = >^/.¹c²+c², y_Q = h ^Txz    y-rti

Obliczamy całkę wewnętrzną

L**-t JJ^ih' ■*-*>*•*

^Txz *" ^JyN    a:²+s²<A²

a otrzymaną całkę podwójną sprowadzamy do współrzędnych biegunowych (podstawiamy x= gcos<p, z — psingp i zastępujemy dxdz przez ędtpdę; we współrzędnych o, ę? równanie okręgu ^4-z² = h² ma posta'

<? = *)

2 n    h

K = y f J (h²- Q²)od(fdo — yj d(p ) (h²Q — Q³)dQ =

o o

2-i

-ł/[

2

6

4 io

nh⁴

4

363