freakpp013

24

pemtury zmienia się w czasie wewnątrz systemu, a na jego powierzchni jest stałe; T(t,x,y,z) = idem (rys. 1.7a przedstawia kąt <p jako nachylenie stycznej do krzywej rozkładu temperatury w danym punkcie A w czasie Bj, B₂, B₃ ... od

mienia ciepła; q_n = -X

powierzchni A do wnętrza ciała). Nie znana jest wartość kąta <p i gęstość stru-3T

dn

II. Warunek brzegowy drugiego rodzaju (warunek Neumanna) Dany jest rozkład strumieni ciepła na powierzchni ciała:

(1.21)

gdzie:--składowa gradientu temperatury w ciele stałym w kierunku ze-

3n

wnętrznej normalnej do jego powierzchni, q_s - strumień ciepła dopływający do powierzchni.

Kąt a musi być podany (rys.l.7b), temperatura, czyli funkcja T(t,x,y,z)|_A nie jest określona.

III.    Warunek brzegowy trzeciego rodzaju

Dana jest temperatura T_f płynu otaczającego ciało A i współczynnik przejmowania ciepła a. Elementarna gęstość strumienia ciepła dq_s między elementarną powierzchnią dA ciała i otaczającym płynem musi być równa elementarnemu strumieniowi ciepła przewodzonego na elementarnej powierzchni rozpatrywanego ciała, co odpowiednio można zapisać:

(VT)_W=|(T_W-T_f)    (1.22)

IV.    Warunek brzegowy czwartego rodzaju

Sprowadza się do równości temperatury powierzchniowej oraz równości elementarnych strumieni ciepła na elementarnej powierzchni oddzielającej dwa ośrodki ciała stałego (rys. 1.7d), jeżeli nie występuje opór kontaktowy, co odpowiednio można zapisać:

(1.23)

T_wi(0- T_w2(t)

ora z

1.5. Pomiar przewodności cieplnej

Z prawa Fouriera (1.1)

X =

q

VT

(1.25)

lub w postaci skalarnej

(1.26)

i ₌__S_

dT/dn

gdzie n - kierunek normalny.

Pomiar wielkości występujących po prawej stronie równania jest niewykonalny. Dlatego do wyznaczenia X używa się rozwiązań pola temperatury dla danej geometrii. Nieustalone i ustalone pola temperatury narzucają podział metod pomiaru X odpowiednio na metody nieustalone i metody ustalone. Najprostsze rozwiązania aparatów pomiarowych dotyczą nieograniczonej płyty o grubości 5, rury i modelu ściany sferycznej, poddanych działaniu ustalonych pól temperatury.

1.5.1. Aparat Poensgena

Pomiar X w aparacie Poensgena opiera się na rozwiązaniu pola temperatury podczas jednokierunkowego (oś x), ustalonego przewodzenia ciepła dla modelu nieograniczonej płaskiej płyty o grubości 5, jak na rys. 1.8, gdzie T_w oznacza temperaturę ścianki.

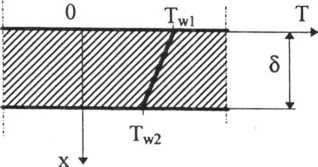
Rys. 1.8. Model płyty w pomiarze X