363 (23)

2) Obszar W ograniczony daną powierzchnią jest elipsoidą obrotową (rys. 183). Rzut W_XJ obszaru na płaszczyznę xOy jest kołem x²+y² < a². Stosując wzór (♦), otrzymamy

' r r

J = J J dxdy f (x²+y²+z²)dz

^wxy    ^XmlN

gdzie zs i *q — wartości z obliczone z równania elipsoidy:

-n,q § W3(a²-x²-y²).

Rys. 182

Obliczamy całkę wewnętrzną (całkę jednokrotną względem z) J

Cv²i-r)c-!-

^Q<Ixdy = 2a²1/3 JJ /a²—x²—y²dxdy

•• xy    AT^J+y^ł<O^ł

Z kolei, aby uprościć obliczenie otrzymanej całki podwójnej sprowadzamy ją do współrzędnych biegunowych. Podstawiając * = pcos<p, y — psinę? i zastępując dxdy przez qd(p dq, otrzymamy

J = 2rr j 3 J f) a²—q² qd(pdq

<?<	a
2*	0
a
V	U
J/i r	2(a^2~
J 0	3
*^2+y^2 ~~ a

dt_P~

2a* j/3

f . w

J *“7T

(równanie okręgu -- a² w tych współrzędnych ma postać p ~ o).

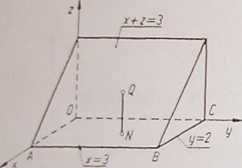
3) Dane powierzchnie ograniczają stożek T, przedstawiony na rys. 184. Każda prosta, przechodząca przez punkt wewnętrzny stożka równolegle do osi- Oy, przecina jego granicę tylko w dwóch punktach, a rzut T_x. stożka na płaszczyznę xOz jest kołem x²-r z² < li². Biorąc to pod uwagę,

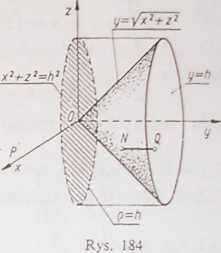
przekształcamy wzór (*), zamieniając rolami zmienne z i y. Otrzymamy wówczas

^ymyQ

K — J J dxdz J ydy,    gdzie: y_s = )    y_Q = h

Obliczamy całkę wewnętrzną

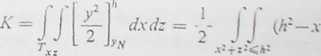
a otrzymaną całkę podwójną sprowadzamy do współrzędnych biegunowych (podstawiamy x = QCosg>, z = psinę? i zastępujemy dxdz przez Qd<pdQ\ we współrzędnych q, <p równanie okręgu = A² ma postać 6 = /»)

J 1 (Ir —Q^2)gdqfdo =	rf
	0
2n .
	i

.t/i⁴

363