2 3 (2)

	Piotr Bieranowski - ćwiczenia z WYTRZYMAŁOŚCI MATERIAŁÓW, CZ. II	2015/16

Podstawiając (2) i (3) do (1) otrzymujemy prawo Hooke'a

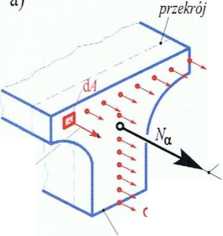
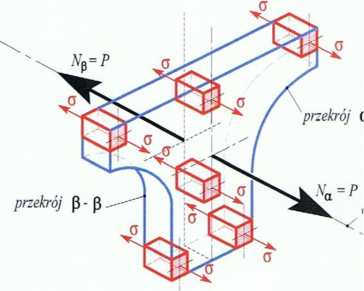
Rys. 2. Określenie naprężeń przy rozciąganiu

e- — lub cr = Es,    (4)

E

Opisujące ogólną zależność fizyczną - oderwaną od wymiarów pręta. Sens tego prawa dogłębnie można zrozumieć rozpatrując plasterek pręta (rys. 2) wycięty poprzecznymi przekrojami a - a i fi - P i podzielony podłużnie na szereg kostek. Każda z tych kostek ma wydłużenie s na kierunku normalnym (prostopadłym) do tych ścian, na których działają naprężenia normalne - oznaczone małą grecką literą cr. Opisywany układ ujmuje wielkości g i e, lecz nie wiąże ich z prętem, tylko z elementarną (podstawową, jednostkową) kostką i pewnym jej przekrojem (ścianą na kierunku normalnym do działającej siły rozciągającej) . Mając na względzie, że wzór Hooke'a jest słuszny tylko w pewnych zakresach granicznych obciążeń (w zależności od rodzaju materiału), możemy prawo Hooke a sprecyzować i jednocześnie wyrazić stwierdzeniem, że w pewnym zakresie wartość naprężenia normalnego do przekroju jest proporcjonalna do wartości względnego wydłużenia w kierunku prostopadłym do tego przekroju.

Wzór (4) unaocznia, że moduł Younga E wyrażony jest w tych samych jednostkach co naprężenie cr, a więc w [MPa] lub [kG/cnr j. Po ujednoliceniu norm europejski w 2010 r. (z PN do PN-EN i PN-EN ISO), spotyka się inny, tożsamy zapis miana [N/mm²]. Tenże wzór

str. 3

P-P

os pręta

acU

= const przekrój a-a

b)