1tom270

10. TECHNIKA WYSOKICH NAPIĘĆ 542

Tablica 10.11 (cd.)

Ro	dzaj mechanizmu			Czynniki warunkujące	Kryteria i podstawowe zależności	Uwagi i objaśnienia
	przebicie czysto jonizacyjne			niejednorodność dielektryka, zanieczyszczenia,, wtrąciny gazowe i płynne, szczeliny; wyładowania nie-zupełne, ich wielokrotne zapłony przy napięciu przemiennym i kumulacja prze-bić częściowych; zmiany chemiczne		Ua — napięcie krytyczne układu, napięcie zapłonu wyładowania: Eia — natężenie krytyczne we wtrącinie; a. a, - grubości dielektryka i wtrąciny; e,ą przenikalność wtrąciny i di-elektryka; C, n współczynniki liczbowe; Uj - napięcie jonizacji; U. — napięcie zapłonu wyła-dowań; Ua napięcie gaśnięcia wyładowań; Ca2 pojemność szeregowa z wtrąciną; qp — ładunek pozorny wyładowania; t. czas żvcia dielektryka; A B — stale liczbowe; T - temperatura bezwzględna; rVi—czas życia w temperaturze T0: m — 0.0S65 — stała Montsinge-ra
		joniza-	u		okres starzenia bczerozyjnego: i = CE~", U Uj
		cyjnc	2)		11, - > o, u > Uj
>» £ o ‘5 g rt		cieplne			t: = Anp^j t. = roiexp T—mt7 — 273)]
Ó a o 3 c o	starzenie	elektroche miczne			T -T ti = t0A~^r~
^n Bezerozyjne. ^21 Z erozją przechodzącą w drzcwicnic (szybka degradacja).

W ocenie wytrzymałości elektrycznej rzeczywistych układów izolacyjnych podstawową rolę odgrywa zależność napięcia przebicia U_p od czasu do przebicia t_p. Obie wielkości są wielkościami losowymi o dużym rozrzucie wartości i w związku z tym wymagają ujęcia statystycznego, opartego na próbach modelowych.

Probabilistyczny model wytrzymałościowy polega na wyznaczeniu U = f(i ) na podstawie eksperymentalnych rozkładów P_U({/_(J) i P,(t ) z uwzględnieniem odpowiednich przedziałów ufności. Wymaga się. aby użyte do eksperymentu próbki możliwie dokładnie odwzorowywały warunki rzeczywiste. Stosowane są dwie drogi postępowania: pomiar t_p przy próbie napięciem o stałej wartości albo pomiar U_p przy próbie napięciem o narastającej wartości. Do aproksymacji wyników pomiarów jest wykorzystywany rozkład Weibulla w dwuwymiarowej (czas, napięcie) wersji Oudina. Aproksymacja U_p przy t_p = const daje rozkład Weibulla o postaci

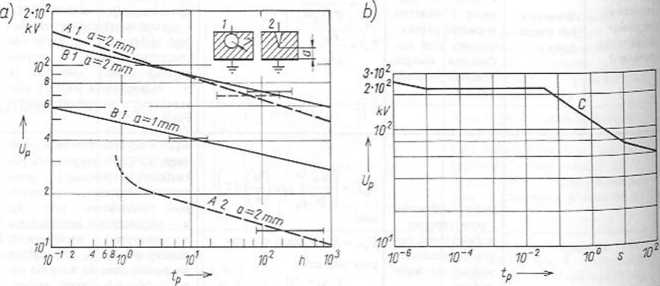
Rys. 10.37. Zależność U_p = /(l_p): a) A    polietylen, B — żywica epoksydowa; b) C — papier bakelizowany (a - 0,3 mm)

w polu niejednostajnym

/ — układ z elektrodą kulową; 2 układ z elektrodą ostrzową

(10.64)

P _u(0'_p) = l-exp

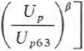
adzie: P.JU_p63) = 0,63; fi = n,k_f — parametr kształtu rozkładu; n, — wykładnik krzywej życia elektrycznego; k, — współczynnik parametru rozkładu.

Zależność U_p =f(t_p) ma postać

__ i_

U_p = C_nt~*    (10.65)

gdzie: C„ — stała zależna od geometrii układu; n, wykładnik zależny od rodzaju dielektryka.

Na rysunku 10.37 przedstawiono w skali logarytmicznej przykładowe charakterystyki wytrzymałościowe U _p = f(i_p) przy założeniu jednego mechanizmu przebicia (n, = const). VV rzeczywistości nie należy się spodziewać charakterystyki jednorodnej w całym zakresie zmian czasu do przebicia (rys. 10.37b). Przy czasach dłuższych niż czas odpowiadający mechanizmowi elektrycznemu następuje widoczne zmniejszenie wytrzymałości.

10.2.1.8. Wytrzymałość układów złożonych

Wytrzymałość układów izolacyjnych, zawierających więcej niż jeden dielektryk, jest warunkowana zmianą rozkładu pola w stosunku do rozkładu wynikającego z geometrii elektrod i zjawiskami zachodzącymi na powierzchniach rozgraniczających dielektryki. Wśród układów złożonych są rozpatrywane: układy zawierające bariery, układy wielo-elektrodowe, układy narażone na opady i zanieczyszczenia oraz układy skłonne do wyładowań powierzchniowych (ślizgowych).

Bariery prostopadłe do linii największych naprężeń wpływają na wytrzymałość w sposób przedstawiony na rys. 10.38.

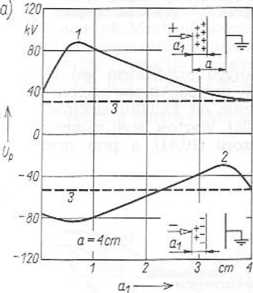
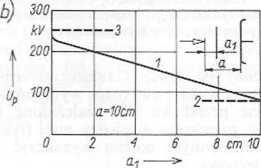
Rys. 10.38. Zależność U_p = /(a.) układu z przegroda: a) przy biegunowości: 1 — dodatniej, 2 — ujemnej (3 — wytrzymałość bez przegrody): b) przy udarach piorunowych (krzywa 1), 2 — wytrzymałość bez przegrody, 3 — wytrzymałość układu o polu jednostajnym

Układ wieloelekirodowy, którego przykładem jest łańcuch izolatorów kołpakowych (rys. 10.39b), charakteryzuje się nierównomiernością rozkładu napięcia między elementami składowymi (rys. 10.39d). O rozkładzie decyduje ich pojemność (rys. 10.39c). W rezultacie napięcie przeskoku U_p całego układu jest niższe niż wynikałoby to z wytrzymałości pojedynczego ogniwa U_pi. Poprawę sytuacji można uzyskać przez

zestopniowanie pojemności szeregowej C_s„ = \c.(n² + n), gdzie n — kolejny numer

n

°gmwa, albo przez wprowadzenie pojemności równoległej (ekranu) C.„ = C.-, adzie

ⁿo — łączna liczba ogniw.