1tom275

10. TECHNIKA WYSOKICH NAPIĘĆ

552

nych z najwyższym napięciem wyposażenia, zgodnie z danymi zawartymi w tabl. 10 14 i« i 10.16.    ■ iffłf

Procedura konwencjonalna polega na stosowaniu marginesu koordynacyjnego, defini wanego jako różnica napięcia między poziomem podstawowym i poziome° ochrony. Margines ten określa współczynnik ochrony, który powinien być mniejszy _np wartość uznana w praktyce za adekwatną — w całym zakresie czasów do przeskoku luK przebicia izolacji. Postępowanie sprowadza się do porównania i doboru charakterystyk udarowych (napięciowo-czasowych) zarówno izolacji, jak i ochronników. Na rysunku 10.47 podano przykład prawidłowego i nieprawidłowego doboru charakterystyk (zakres-kowany obszar rozrzutu). W przypadku nieprawidłowego doboru charakterystyk, przy czasie narastania przepięć l_p > rj, (rys. 10.47a) — brak jest w ogóle ochrony, natomiast przy bardzo krótkim czasie margines może okazać się zbyt wielki. Przy prawidłowym doborze charakterystyk zaleca się, aby przedziały wyznaczające rozrzut wytrzymałości koordynowanych urządzeń zawierały wspólne wartości z prawdopodobieństwem na poziomie 10%. Rozszerzenie marginesu koordynacyjnego (MK na rys. 10.47b) prowadzi do wzrostu kosztów izolacji, a zawężenie do zbyt częstego wyłączania urządzeń.

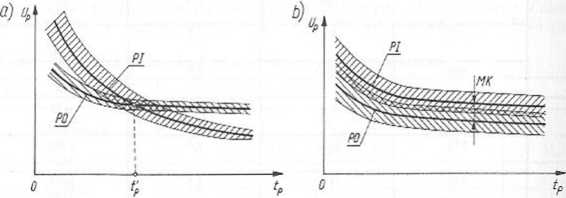
Rys. 10.47. Charakterystyki udarowe układów skoordynowanych: a) nieprawidłowo; b) prawidłowo PI — poziom izolacji, PO poziom ochrony, MK margines koordynacyjny

Procedura statystyczna zakłada możliwość występoyvania uszkodzeń izolacji na określonym poziomie ryzyka R, stanowiącego wskaźnik zagrożenia (rys. 10.48a) zdefiniowany jako

oc

R = \g(U)P(U)dU    (10.75)

0

gdzie: g(U) — funkcja gęstości rozkładu prawdopodobieństwa określonego rodzaju przepięć; P(l/) — dystrybuanta napięć przeskoku.

Przy założeniu rozkładu normalnego

9(U)

oraz

dG(U) _    1 f (c/-D-_5Dn

d O    2<r² J

(10.76)

P(O) = •

J exp

y/2%0 -cc

[4

-Ł/,

d.v

(10.77)

i a — odchylenie standardowe ustalone na (10.52) i (10.53). Najczęściej przyjmuje

przy czym: U₅₀ — wartość przeciętna

podstawie pomiarów wg zależności _v_____, . _v__________{a r}—_r. .    _

o < 0,08 U,50 dla udarów łączeniowych i a ^ 0,05 Vdla udarów piorunowych.

W przypadku funkcji g(U) mogą wystąpić również inne rozkłady, jak rozkład logary^trn no-normalny lub rozkład Weibulla.

Zwykle amplitudę przepięć U_m zastępuje się wartością współczynnika przepięć

k_p= I———, gdzie U,_m — wartość skuteczna najwyższego napięcia roboczego. Na V2 U_rm    .....

rysunku 10.48b przedstawiono krzywe g,(k_p) i G₍(k_p) — typowe dla przepięć łączeniowych

1    krzywe g_p{k.) i G_p(k ) — typowe dla przepiec piorunowych. Rzędne skumulowanych rozkładów Cj_t(k_p) i G_f(/c„) przy k_p = k_a określają prawdopodobieństwo wystąpienia większych krotności przepięć niż fc„. Odpowiadają im obszary zakreskowanc pod krzywymi g_l(k_l) i g_p(k_p). W praktyce zastosowanie znajduje uproszczona procedura statystycznej koordynacji izolacji, w której wykorzystuje się fakt, że przy określeniu ryzyka Przeskoku można posłużyć się odpowiednio wybranymi wartościami znanych rozkładów 9{V) i P(U). Dotyczą one dwu charakterystycznych wielkości: stytystycznego przepięcia "s i statystycznej wytrzymałości udarowej U„.

Przepięcie statystyczne L'_}jest definiowane jako wartość, która może być przekroczona

²    określonym prawdopodobieństwem, np. ustalonym na poziomie 2%. Przy tej wartości ^w rozkładzie normalnym: G(UJ = 0,02 oraz U_so = C/_s—2,054er_s i wówczas

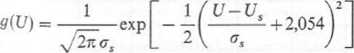
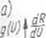
6)

W g(M„)

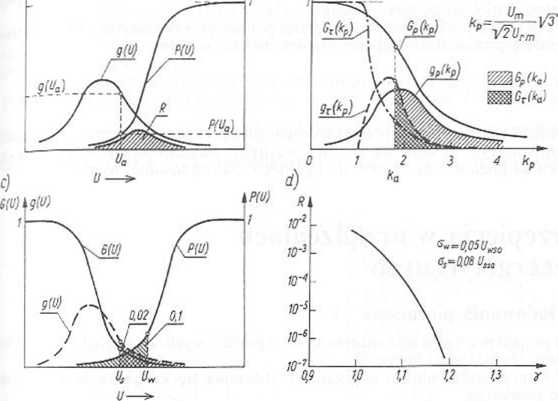
Rys. 10.48. Krzywe charakteryzujące ryzyko uszkodzenia izolacji: a) ilustracja określenia ryzyka; b) rozkłady przepięć piorunowych i łączeniowych; c) ilustracja przepięcia statystycznego U_s i wytrzymałości statystycznej d> zależność ryzyka od statystycznego współczynnika bezpieczeństwa (ochrony)

(10.78)

Wytrzymałość udarowa statystyczna U„ jest definiowana jako wartość szczytowa “daru, która nie powoduje przeskoku z określonym prawdopodobieństwem, np. ustalony¹¹¹ na poziomie 90%. Wartość U_w = U_vn odpowiada 10%-napięciu przeskoku. Przy tej drtości w rozkładzie normalnym: P(t/J = 0,1 oraz t/₅₀ = U_w+ 1,28 l<r_w i wówczas

P(D) =

U

I ^exP

2k (7_h, -oo

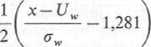
2

dx

(10.79)

v