1tom277

10. TECHNIKA WYSOKICH NAPIĘĆ

Istotną wielkością w ocenie zagrożenia piorunowego jest roczna gęstość wyładowań piorunowych (odniesiona do 1 km- powierzchni terenu)

N, = *N$    (10.81)

przy czym: N_d — poziom izokerauniczny lub inaczej liczba dni burzowych w roku na danym terenie; a i — współczynniki liczbowe.

Warunkom polskim odpowiadają wartości: N_d — 13 ^ 34, z = 0,036 i /? = 1,3, a zatem N_r — 1,0 —3,5. Znajomość N_r pozwala wyznaczyć roczną liczbę A' trafień piorunowych w obiekt. Dla obiektu w' kształcie prostopadłościanu lub dającego się opisać prostopadłościanem o wymiarach poziomych a, b (w metrach) i wysokości h < 50 m

N = N_r[ab + 26,8(a+b)h⁰-⁵ + 564K] ■ 10~⁶    (10.82)

W przypadku, gdy obiektem jest linia elektroenergetyczna o długości 100 km (a = 0, 6= 10’ m) w rejonie rów'ninnvm kraju, można przyjąć, że A' = l,8/(km² a) oraz N = 4,8h°‘.

Prawdopodobieństwo wystąpienia co najmniej jednego trafienia (k > 1) w obiekt w ciągu roku wynosi

P(fc»l) = 1 — exp(—Ai')    (10.83)

Gdy N « 1, wówczas P(k > 1)« N. Jeżeli ponadto przyjąć, że każde trafienie może z prawdopodobieństwem P_s wywołać szkodę, to prawdopodobieństwo (lub ryzyko) wystąpienia szkody w ciągu roku można wyrazić zależnością

R = 1 -exp(-ATPJ w NP_S    (10.84)

Wartości P_s wynikają z oceny skutków na tle rozkładu parametrów wyładowań piorunowych i podatności obiektu na uszkodzenia. W przypadku budynków będą to głównie uszkodzenia mechaniczne i porażenia oraz zapłony materiałów palnych i wybuchowych, zaś w przypadku linii elektroenergetycznych — przepięcia i powodowane nimi przebicia układów izolacyjnych.

10.3.2. Przepięcia atmosferyczne

Należy wyróżnić uderzenie pioruna w pobliżu linii (rys. 10.51a) i uderzenie w jeden z jej elementów. W pierwszym przypadku powstają przepięcia indukowane, rzadko przekraczające wartość 200 kV, w drugim zaś — oprócz przepięć indukowanych — znacznie od nich większe przepięcia bezpośrednie (tabl. 10.19).

Przepięcia bezpośrednie zależą od układu linii i od elementu, w który uderza piorun. Można wyróżnić 4 przypadki:

1.    Uderzenie pioruna w przewód roboczy o impedancji falowej Z (rys. 10.51 b). Prąd pioruna I_p dzieli się na dwie równe części, z którymi jest związane napięcie

U\ =    0,5 ZI_p    (10.85)

W typowej linii napowietrznej (Z = 500 H), przy przeciętnym prądzie piorunowym I_p = 25 kA, U\ = 6,25 MV. Nie ma najmniejszej szansy, aby izolacja linii tę wartość wytrzymała.

2.    Uderzenie pioruna w przewód odgromowy o impedancji falowej Z_} w pewnej odległości od słupa (rys. 10.5 lc). Napięcie na trafionym przewodzie przyjmuje—jak poprzednio — wartość

U\ =    0,5 ZJ_p    (10.86)

a na przewodzie roboczym, o impedancji falowej Z₂, wartość indukowaną U'₂ =    kU\    (10.87)

przy czym k — współczynnik sprzężenia obu przewodów.

Przy h » a (rys. 10.5 lc)

(10.88)

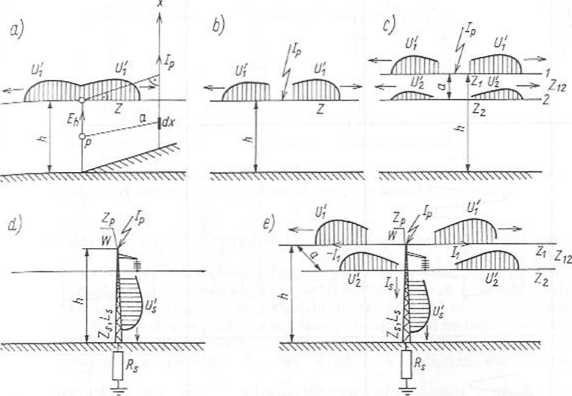
Rys. 10.51. Szkic ilustrujący powstawanie przepięć przy uderzeniu pioruna: a) obok linii; b) w przewód roboczy linii; c) w przewód odgromowy linii; d) w słup bez przewodu odgromowego; e) w słup z przewodem odgromowym

Z₁₂ ln2h—Ina Z_x In2/i —lnr

gdzie: Z₁₂ — impedancja układu obu przewodów; r — promień przewodu odgromowego.

Napięcie Ł/_I2 na izolacji linii wynika z różnicy napięć U\ i U'₂, a więc

U_l2 =(l-k)U\    (10.89)

Jeżeli napięcie to okaże się większe niż napięcie wytrzymywane przez izolację, to nastąpi przeskok od części uziemionej do izolowanej, zwany przeskokiem odwrotnym.

3. Uderzenie pioruna w wierzchołek słupa linii bez przewodu odgromowego (rys. 10.51d). Zadanie sprowadza się do obliczenia napięcia wierzchołka słupa albo metodą wielokrotnych odbić fal na jego krańcach w'g p. 10.3.4 albo metodą obwodu zastępczego zgodnie z uproszczoną zależnością

U_w = R_sI_p+L/^f)    (10.90)

Y Cif Jmax

w której: L_s, R_s — indukcyjność i rezystancja uziemienia słupa; I_p—wartość szczytowa prądu pioruna i_p.

Pod wpływem tego napięcia może dojść do przeskoku odwrotnego na izolowanej linii, gdy przekroczona zostaje jej wytrzymałość U_u. Przez porównanie U_w z U_u można wyznaczyć maksymalną wartość R_s, przy której nie wystąpi jeszcze przeskok odwrotny.

4. Uderzenie pioruna w wierzchołek słupa linii z przewodem odgromow'ym (rys. 10.51e).

Z

Prąd pioruna l_p dzieli się na prąd w przewodzie odgromowym I_L    -—l_p

Zj +2 Z_s