266

1203.

1203.

dy

dx

+ 2>>+32=0

dz

*^+J,=0

1204.

—2w— 4o = cos dt

^r- +u-\-2v = sini dt

du ,    „

dx

1205.    4^C- — «+»—w = 0

dx

dw    _n

—---u—v—w = 0

dx

Znaleźć rozwiązania szczególne układów równań, spełniające podane obok warunki początkowe:

1206.

^+3*+, = 0

x(0) = l,    y(0) = -l

—x+y = 0

1207.

-4^—|- 4zj = cos2x dx

dv

dx

-j-4« = sin2x

_M(0) = 0, ®(0) - 0,1

§ 14. Równania fizyki matematycznej

Wiele zagadnień fizycznych prowadzi do liniowych równań różniczkowych o pochodnych cząstkowych drugiego rzędu; nazywają się one dlatego równaniami fizyki matematycznej.

Podstawowymi równaniami fizyki matematycznej, w przypadku gdy funkcja szukani zależy od dwóch zmiennych niezależnych, są:

I. Równanie falowe

8²u    ₂ d²u

— ćT-r-r = 0

dt² coc²

będące najprostszym równaniem o pochodnych cząstkowych drugiego rzędu typu hiperbolicznego. Do rozwiązywania takiego równania sprowadzają się zadania o drganiach poprzecznych struny i o podłużnych drganiach pręta, o drganiach akustycznych i elektromagnetycznych, o drganiach gazu i wiele innych zadań dotyczących rozchodzenia się drgań w ośrodku jednorodnym.

II. Równanie przewodnictwa cieplnego

Bu , B¹u

~Bl~^a~BJ

będące najprostszym rodzajem równań o pochodnych cząstkowych drugiego rzędu typu parabolicznego. Do rozwiązywania tego równania sprowadzają się zadania o rozchodzeniu się ciepła w ośrodku jednorodnym, o dyfuzji cieczy albo gazów i wiele innych zagadnień.

III. Równanie Laplacea

= 0

B²u B²u ⁺ ~B?

będące najprostszym równaniem o pochodnych cząstkowych drugiego rzędu typu eliptycznego. Do rozwiązywania tego równania sprowadzają się zadania dotyczące własności stacjonarnych pól elektromagnetycznych, stacjonarnego rozkładu ciepła w ciele jednorodnym, potencjału prędkości bezwirowego przepływu cieczy i wiele innych zadań. w których określamy własności stacjonarne (ustalone w' czasie) procesów.

Zagadnienie całkowania równań o pochodnych cząstkowych, czyli

zadanie wyznaczenia funkcji spełniających to równanie ma nieskończenie

» • • wiele rozwiązań. Na przykład, równanie-^^- = 0 można napisać w postaci

Su

dx

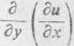
= 0, skąd wynika, że

nie zależy od y i jest pewną do

wolną (różniczkowalną) funkcją jedne; tylko zmiennej x, czyli — ~/(x). Całkując tę równość względ' x, otrzymamy u = F(x)-r C. Stała całkowania C jest stałą względem a noże jednak być ona dowolną (różniczkowalną) funkcją zmiennej y, czyli C - (p(y). Dlatego ogólnym rozwiązaniem danego równania o pochodnych cząstkowych drugiego rzędu będzie wyrażenie zawierające dwie funkcje dowolne: u = F{x) f ?00- Podstawiając zamiast dowolnych funkcji F i (p różne określone funkcje można z rozwią-

535