8210

Rysunek tutaj, pdydz - (p + ^ dx)dydz; pdzdx - (p + ^ dy)dxdz_: pdydx - (p + ^ dz)dydx c)x    dy    dz

dy    dy

Mnożę siłę składowa z masy elementu z --—-i pdxdydz;__I pdxdvdz •

dr    dr

d y

--LŁ pdxdydz Gdy układ sil jest w równowadze to zgodnie z zasada De' Alamberta suma rzutów

dt

sił = 0; xpdxdydz - ~ dxdydz = —— pdxdydz = 0» dx    dt

ypdxdydz - — dxdydz =--— pdxdydz = 0; zpdxdydz - — dxdydz - -    pdxdydz = 0

dy    dt    dz    dt

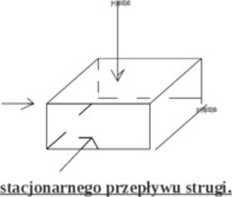
■^JRównąnte Bernoulieęo dla jednowymiarowego

dv/dt+v^ł,dv/ds=GS-(l/ro)^,'^,dp/ds+(lambda*g^,,,v²/2D). Pole grawitacyjne: v*dv/ds.-GS+l/ro*dp ds-i (lambda^,"g^,V²/2D)=0; Mi*dv²/ds+g*dz;ds+(lambda^,,'g^,'‘v²/2D)=0 /*ds.;

* dv-+gdz+dp/ro+( lambda^g^^Dj^ds^O; J d(—v“ + gz + ~) + J-^-ds ⁼ ® ;

— + gz + — +1 —^—ds = 0;A = 0, v = 0_; v*/2+p ro+gz=const; dla cieczy rzeczywistej

2    p ^J 2D

v²/2+p^,ro+gz+(Iambda^4,gV^!/2D)+(£'*v^:,4'^2)=const; dla gazu v²/2+g^,ł,dp/ro+gz=const

RTliip ; i=p,RT

pv=(z)RT; v=l/ro; p/ro=RT(z): T = const

v² _ jdpRT

p=IRT(z); v = 2RTln — V    Po

B erno uliego dla płynu idealnego,

V=0; dv/dt=0 - przyśpieszenie lokalne; rotv =0; dv/dt=g=l/ro* ▼ p; dv/dt=(v^4,v)^,4v=g-(l, ro)^4, T p Z analizy matematycznej: (v*v)=l/2'*^,v^,^v²+v*rotv; Vi+V *v²-g-(l/no) * Tp^O ; g=-Tn Vi+ ▼ ⁺ v • vn f ▼ p=0; 1/ro ▼ = ▼ p; ro=const; 1/ro ▼ p= ▼ p/ro; v²/2+n+p=const; ^72+11+ p/ro=const n=g,; v*/2+g«+ p/ro=const

Równanie Bernouliego - przemiana gazowa; R - indywidualna stała gazowa;_pV=nRT;_p p=RT/p z tego p=pp/RTi_V=-m/p ; n=m/p ; R=R*MLpm/p=m R*pT/pi p/p= RTip=p/RT / J dp

v    ; R’T Jdp/p + v*/2 = const; R*T In I p I Wl2 = const

const ^J    |K|

R T 2

27 Równanie ruch płynu doskonałego (równanie Eulera! wyprowadzone z równowagi sił

Równanie ruchu płynu doskonałego wynika z zasady zachowania pędu, gdzie pochodna płynu zawartego wewnątrz obszaru V względem czasu jest równa sumie sił zewnętrznych czyli:

Jdpp + v²= const;