mech4b1 jpeg

mech4b1 jpeg

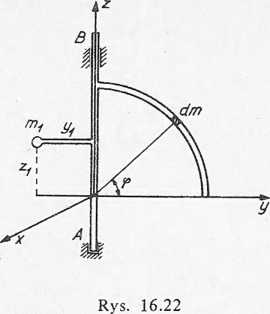
D_x = / yz dm, D_y = / xz dm = 0. (m) (m'

Pisząc równanie parametryczne krzywej

te | re

y = r cos a, z = r sin a, 0 < ip <

możemy obliczyć moment dewiacji pręta

^Dix ⁼ p tT ^{r2 cos} V ^sin 0 ^r ^ ⁼ {p ^f3> 0

m

gdzie p = —--, więc

2 ^r

i moment dewiacji układu

D_x = m n r² + m₁ yj Zj. Współrzędne środka ciężkości pręta będą równe:

x_c 0,

yc

S y^dm

(m)

m

= — p ,/ r cos r d y = — r m ° m

2_r_

TT

Wyszukiwarka

Podobne podstrony:
mech4b jpeg 473 Dx = S yz dm, D = S xz dm = 0. (m)    (m Pisząc równanie parametrycz
15346 P1020223 J = p& + ?)nr r x = r cos cp y = r sóup dm = pdV = pdxdydz dx ——= cos <p
Image3092 3F 3F du dv = df df dx1 dy dx dx du dv dy dy du dv 2e2xcosyJ-e2xsiny 2 u -
img111 121 * 2 fyjź (*.y#2)dy*dz ■ 2X(dx)2 ♦ 2x(dy)2 4 2x(dz)2 A Z8ten różniczkę d2£ Jest * punkcie
img111 121 * 2 fyjź (*.y#2)dy*dz ■ 2X(dx)2 ♦ 2x(dy)2 4 2x(dz)2 A Z8ten różniczkę d2£ Jest * punkcie
skan0017 Wyznaczyć całki ogólne następujących równań różniczkowych!
Xdx--^-dx = 0, p dx Ydy--^-dy = 0; P fy Zdz-- — dz = 0. p dz Z kolei, sumując te równania stronami,
76 (177) 112 Turbo Pascal • Ćwiczenia praktyczne begin if (X+dX>-l) and (X+dX<-80) and (Y+dY&g
Zdjęcie1208 •mu mmmnm tr**dM cf» HMfOpt m wm( iwfpnf    te%dM męm&m m almoM ^wwwf
Image3092 3F 3F du dv = df df dx1 dy dx dx du dv dy dy du dv 2e2xcosyJ-e2xsiny 2 u -
204O 205 dX=ł0.004 dY=+0.012 dH=-0.016 ° dX=+0.017 dY=ł0.060 dH=-0.127o
Rysunek tutaj, pdydz - (p + ^ dx)dydz; pdzdx - (p + ^ dy)dxdz: pdydx - (p + ^ dz)dydx
ZBIGNIEW BLOCKI (ozn. ux = du/dx, uy = du/dy). Zauważmy, że każda funkcja C-różniczkowalna jest
Pizelew (upust) wieżowy Płaskie filtracje ustaloneVX-kd± dx Vy = -k— dy Potencjał prędkości <p
Str 018 to znaczy adt + a dy + a, Az = 0. x    y    z Jest to rów

więcej podobnych podstron