269

(7)

Rozwiązaniem będzie również suma rozwiązań szczególnych

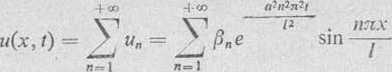
Korzystając z trzeciego warunku: u — <pfa), gdy t — 0, otrzymamy równość

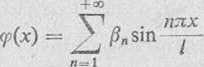
z której możemy określić /?„. Równość ta jest rozwinięciem danej funkcji <p(x) w przedziale (0, /) w niepełny szereg Fouriera według samych tylko cosinusów. Na podstawie wzoru (*), znajdujemy

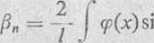
. rmx sin —j—

o

(8)

Wobec tego suma szeregu (7), którego współczynniki są określone wzorami (8), jest szczególnym rozwiązaniem danego równania, spełniającym nałożone warunki graniczne.

Sens fizyczny rozwiązanego zadania można przedstawić następująco: jednorodny pręt o długości I, którego powierzchnia boczna nie przewodzi ciepła, pokrywa się z osią Ox, a jego końce znajdujące się w punktach x = 0 i x = / są utrzymywane w stałej temperaturze u = 0. W chwili początkowej t = 0 rozkład temperatury wzdłuż pręta jest znaną funkcją u = <pfa). Rozważane równanie opisuje proces rozchodzenia się ciepła

w pręcie (parametr a¹ — - , gdzie k — współczynnik przewodnictwa

CQ

cieplnego pręta, c —pojemność cieplna materiału, o — gęstość pręta), a otrzymane rozwiązanie u(x, t) tego równania określa rozkład temperatur wzdłuż pręta w dowolnej chwili czasu.

Rozchodzeniu się ciepła w pręcie o nieograniczonej długości (nieskończonego w obu kierunkach) odpowiada takie samo równanie różniczkowe (II), z jedynym warunkiem początkowym: ufa, 0) = <pfa)\ — co <x < określającym rozkład temperatury pręta w chwili początkowej / = 0.

W myśl metody Fouriera, zakładając u = Xfa)T(t), także i dla tego zadania otrzymamy rozwiązanie szczególne o postaci

u = e

(«cosża:+/?sinŻA-)

(9)

W tym przypadku jednak parametr X ma zupełnie dowolne wartości, nie ma bowiem żadnych podstaw (warunków), aby można było wybrać pewne określone jego wartości. We wzorze (9) X może więc zmieniać się od —co do +co. Zatem rozwiązaniem tego zadania będzie nie suma szeregu utworzonego z rozwiązań szczególnych, jak w poprzednich zadaniach, lecz całka niewłaściwa względem parametru X

+ 00

/•—a² A²/

e    (ot cos 2*+/? sin Ax)<fźl    (10)

— 00

Aby wyznaczyć współczynniki ot i /?, wykorzystując nałożony warunek u(x, 0) = <p(x), podstawiamy t — 0 i u = ę>(x) do równości (10). Mamy

+ CC

<p{x) = | (mcos Xx -{-/? sin Xx) <7/

- co

Porównując otrzymaną równość ze wzorem Fouriera (rozdz. IX, § 8) dla funkcji q>(x)

+ co +oo

<7'(or) = — | ||^ | ęnr)cosAz<fejcosXx~

— co — oo

+ 00

+

j f(z) sin/zć/zj sin Az j dX

znajdujemy dla u i p następujące wyrażenia

+ 00    * +00

a(X) = j <p(z) cos Xrdz,    p(X) =-^ | tp(z)s\nXzdz (11)

— CO    —00

Zatem szukane rozwiązanie szczególne danego równania, spełniające dany warunek początkowy, czyli rozwiązanie zadania o rozchodzeniu się ciepła w pręcie nieograniczonym, ma postać całki niewłaściwej (10), przy czym a i p są określone wzorami (11).

541