336 337

336 Zarządzanie projektami

czynności niekrytycznych dla omawianego harmonogramu przedstawiono w formie niewypełnionych prostokątów. Po dokładniejszym przyjrzeniu się harmonogramowi przedstawionemu na rys. 7.8 i porównaniu wielkości rezerw z rezerwami przedstawionymi w tablicy 7.3 widzimy, że rezerwy dla czynności niekrytycznych mogą się różnić i być od siebie zależne. Dotyczy to czynności B i E. W omawianym harmonogramie czynność B ma rezerwę równą 0, gdyż rozpoczęcie czynności E zaplanowano bezpośrednio po najwcześniejszym zakończeniu czynności B. Wyliczona uprzednio wartość rezerwy dla tej czynności wynosi 5. Gdyby więc okazało się, że w trakcie realizacji projektu wykonanie czynności B trwałoby dłużej niż 7 jednostek (ale przedłużenie to nie przekraczałoby zapisanej w tablicy 7.3 wartości 5 jednostek), to nie wpłynęłoby to na wydłużenie realizacji całego projektu, lecz uszczupliłoby wielkość rezerwy dla czynności E.

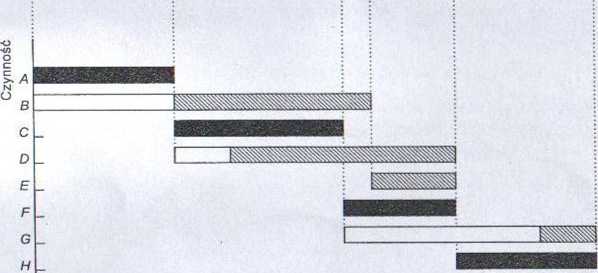
Drugi z przykładowych harmonogramów przedstawiono na rys. 7.9. Przy jego konstrukcji przyjęto, że wszystkie czynności będą się rozpoczynały w najpóźniejszych dopuszczalnych momentach, stąd też nazywany jest harmonogramem ALAP (as late as possible).

Rysunek 7.9

I    I    I    I_I_I_I_I_I_I_t_L-—1_I_I-1-1-1-1-1-►

1    2    3    4    5    6    7    8    9    10 11    12 13    14    15    16    17    18    19 20    „

O ®    ®®    ®    ®

Czas

Momenty zaistnienia zdarzeń są teraz następujące: xi=0, X2 = 5, jc3=I2, X4=ll, x.i=15, X6 = 20.

Momenty zaistnienia zdarzeń związanych z czynnościami krytycznymi nie ulegają zmianie, natomiast zmienia się moment zaistnienia zdarzenia 3.

Czynność B zostanie rozpoczęta po całkowitym wykorzystaniu rezerwy dla tej czynności wynoszącej 5 jednostek. Spowoduje to zmniejszenie rezerwy czynności E do poziomu 0. Zgodnie z omówioną powyżej propozycją konstrukcji

harmonogramu — jak widać — odmienny jest sposób wykorzystania rezerw dla czynności B i E. Należy przypuszczać, że w większości przypadków bezpieczniejszym sposobem realizacji projektu jest sposób opisany w pierwszym z rozpatrywanych harmonogramów.

7.3.5. Zdarzenia i czynności pozorne

Sieć czynności odpowiadająca projektowi powinna być grafem acyklicznym (bez cykli i pętli) oraz mieć dokładnie jeden wierzchołek początkowy i jeden wierzchołek końcowy. Ponadto przy konstrukcji sieci czynności muszą być zachowane następujące zasady:

1.    Dwa dowolnie wybrane zdarzenia może łączyć co najwyżej jedna czynność.

2.    Jednej czynności odpowiada w sieci dokładnie jeden łuk.

Sieć odpowiadająca projektowi opisanemu w przykładzie 7.1 spełniała powyższe warunki. Pokażemy, w jaki sposób postąpić w sytuacji, gdy nie wszystkie przedstawione powyżej warunki są spełnione.

Przykład 7.2²

Rozpatrujemy projekt budowy kortów tenisowych na terenie uczelni, zainicjowany przez organizację studencką. Planowane czynności, kolejność ich wykonania oraz przewidywane czasy trwania (w tygodniach) ilustruje tablica 7.4.

Tablica 7.4

Czynność	Opis czynności	Czynność bezpośrednio poprzedzająca	Czas trwania czynności
A	Pomiar gruntu	—	6
B	Opracowanie projektu wstępnego	—	8
C	Uzyskanie zgody rektora	A. B	12
D	Wybór architekta	C	4
E	Opracowanie budżetu	C	6
F	Opracowanie projektu końcowego	D. E	15
G	Zapewnienie źródeł finansowania	E	12
H 1_	Wynajęcie wykonawcy	F, G	8

² Dane liczbowe przykładu zaczerpnięto z pracy: D.R. Anderson, D. Swccney. T.A. Willimams, An hnroduction to Management Science, Wcsi Publishing Company, 1991.