332 333

332 Zarządzanie projektami

Czynność G można rozpocząć po zakończeniu czynności C, więc:

ES= 11,

EF= 11+2=13.

Czynność H może zostać rozpoczęta po zrealizowaniu czynności D, E i F, czyli moment jej rozpoczęcia nie może być wcześniejszy od najwcześniejszego momentu zakończenia każdej z nich, stąd:

£S=max (13, 10, 15)= 15,

EF= 15 + 5 = 20.

Oznaczymy przez T najkrótszy czas realizacji przedsięwzięcia. Mamy dwie czynności kończące się w wierzchołku końcowym 6: G i H. Ukończenie obu tych czynności świadczy o zakończeniu realizacji projektu, tak więc:

7'=max {13, 20} =20.

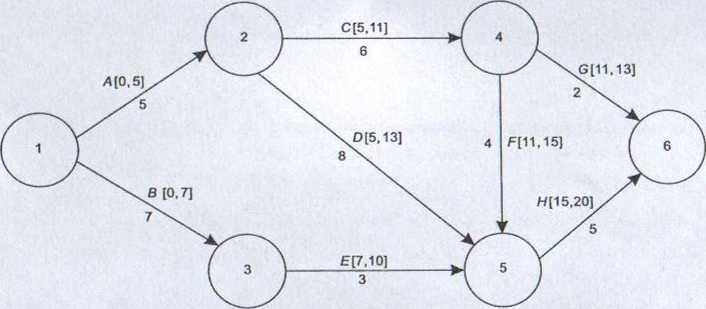
Znalezione momenty ES oraz EF dla kolejnych czynności przedstawiono na rys. 7.6.

Rysunek 7.6

7.3.2. Krok do tyłu

Posługujemy się dodatkowo następującymi oznaczeniami:

LS — najpóźniejszy moment rozpoczęcia danej czynności,

LF — najpóźniejszy moment zakończenia danej czynności.

Zachodzi związek:

LS = LF-t.

Zilustrujemy zastosowanie kroku do tyłu, korzystając ponownie z danych przykładu 7.1. Obliczenia rozpoczynamy od czynności U i G, kończących się w wierzchołku 6. Oczywiście dla tych czynności mamy LF = T= 20.

Czynność H musi zakończyć się nie później, niż wskazuje na to najkrótszy czas realizacji przedsięwzięcia, stąd:

LF-20,

LS=20-5=15.

Czynność G również nie może zakończyć się później, niż wskazuje na to najkrótszy czas realizacji przedsięwzięcia, czyli:

LF =20,

LS= 20-2=18.

Czynność F musi zakończyć się najpóźniej w momencie 15, gdyż jej późniejsze zakończenie spowodowałoby opóźnienie rozpoczęcia czynności H, co oznaczałoby jednocześnie opóźnienie realizacji całego projektu, tak więc:

LF= 15,

15=15-4=11.

Czynność E — podobnie jak rozpatrywana uprzednio czynność F — nie może zakończyć się później niż w momencie 15, aby nie opóźnić czynności H, stąd:

LF= 15,

LS= 15-3=12.

Czynność D również nie może opóźnić czynności H, czyli:

LF- 15,

15=15-8 = 7.

Czynność C musi zostać zakończona tak, aby nie opóźnić następujących po niej czynności F i G, stąd:

LF=min (11, 18) = 11,

LS- 11 —6 = 5.

Czynność B musi się zakończyć napóźniej w momencie 12, aby nie opóźnić następującej po niej czynności E, czyli:

LF= 12,

LS= 12-7=5.

Czynność A nie może opóźnić rozpoczęcia czynności D i C, następujących bezpośrednio po niej, stąd:

LF= min {7, 5} =5,

LS=5 —5=0.