5 (2)

91

Pochodna funkcji rzeczywistej

Podobnie jak poprzednio otrzymujemy

(10)

f'(x) = 2xsin-— cos— (x # 0). X X

Przy x = 0 korzystając z definicji pochodnej mamy

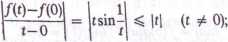
przy t^-»0 widzimy, że

o.

&

W ten sposób funkcja/ jest różnićzkowalna we wszystkich punktach x, lecz/' nie jest funkcją ciągłą, ponieważ cos(l/x) we wzorze (10) nie dąży do żadnej granicy przy x-*Q..

Twierdzenia o wartości średniej

5.7. DEFINICJA. "Niech/ będzie funkcją rzeczywistą, określoną w przestrzeni metrycznej X.Powiemy,że/ ma maksimum lokalne w punkcie p 6 X, jeśli istnieje 5 > 0taka,że/(q) </( p) dla wszystkich q e X takich, że d(p, q) < 6.

W podobny sposób określa się minimum lokalne.

Nasze następne twierdzenie leży u podstaw rozlicznych zastosowań rachunku różniczkowego.

5.8. TWIERDZENIE. Niech funkcjaf będzie określona na przedziale domkniętym (a, by, jeśli f ma w punkcie x e (a, b) maksimum lokalne i jeżeli istnieje f'(x), to /'(x) = 0.

Dowód. Obierzmy d zgodnie z definicją 5.7, tzn. takie, aby o < x~5 < x < x+5 < b. Jefli x—3 < t < x, to

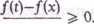
t—x

Przy t dążącym do x widać, że/'(x) > 0. Jeśli x < t < x+S, to

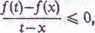
skąd wynika, że/'(x) < 0. Ale to znaczy, że/'(x) = 0. Analogiczne twierdzenie dotyczące minimum lokalnego jest oczywiście też prawdziwe.

5.9. TWIERDZENIE. Jeżeli funkcje rzeczywiste f i g są ciągle na przedziale domkniętym <a, b> i różniczkowalne na przedziale otwartym (a, b), to istnieje punkt x e (o, b), w którym

lf(b)-Xa)Mx) * [g{b)—g(aj]f(x).