810

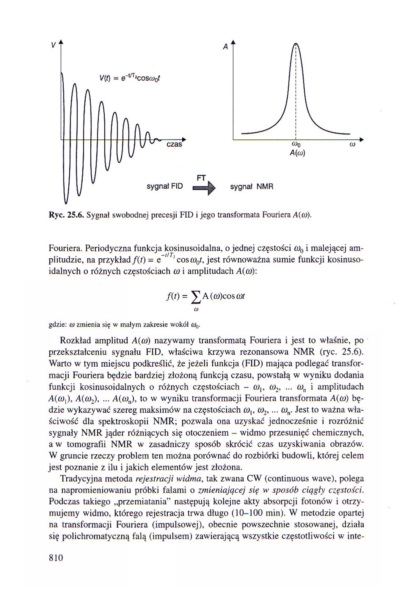
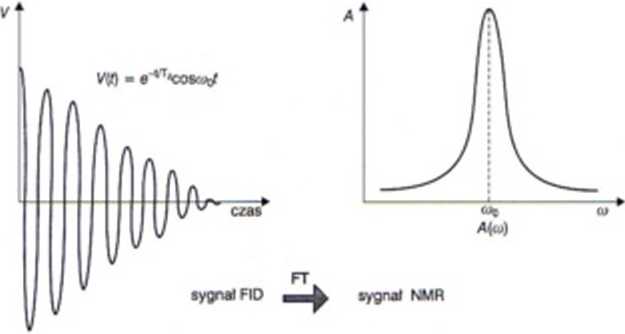
Ryc. 25.*. Sygnał swobodnej precesji F1D i jego transformata Fouriera

Fouriera. Periodyczna funkcja kosmusoidalna. o jednej częstości oą, i malejącej amplitudzie. na przykład /W * c cosoy. jest równoważna sumie funkcji kosinuso-idalnych o różnych częstościach co i amplitudach Mco)

/(/) = £A(o>)cosar

m

$dite iv uimiii wę w miłym ukieuc wokół «*.

Rozkład amplitud /4(oi) nazywamy transformatą Fouriera i jest to właśnie, po przekształceniu sygnału FID. właściwa krzywa rezonansowa NMR (ryc. 25.6). Warto w tym miejscu podkreślić, że jeżeli funkcja (FID) mająca podlegać transformacji Fouriera będzie bardziej złożoną funkcją czasu, powstałą w wyniku dodania funkcji kosinusoidalnych o różnych częstościach - ov tu,. ... i amplitudach >4(01,). >4(0K). ... MitiJ. to w wyniku transformacji Fouriera transformata Ma» będzie wykazywać szereg maksimów na częstościach tu,. <u₂.... ov Jest to ważna właściwość dla spektroskopii NMR; pozwala ona uzyskać jednocześnie i rozróżnić sygnały NMR jąder różniących się otoczeniem - widmo przesunięć chemicznych, a w tomografu NMR w zasadniczy sposób skrócić czas uzyskiwania obrazów. W gruncie rzeczy problem ten można porównać do rozbiórki budowli, której celem jest poznanie z ilu i jakich elementów jest złożona.

Tradycyjna metoda re/estraeji »idma. tak zwana CW (continuous wave). polega nu napromieniowaniu próbki falami o mniemającej sif w sposób ciągły częsioici. Podczas takiego .przemiatania** następują kolejne akty absorpcji fotonów i otrzymujemy widmo, którego rejestracja trwa długo (10-100 min). W' metodzie opartej na transformacji Fouriera (impulsowej), obecnie powszechnie stosowanej, działa się połichromalyc/ną falą (impulsem) zawierającą wszy akie częaatliwości w inte-

810