Bramki logiczne cz2

Układy cyfrowe 37

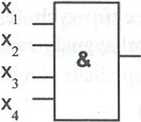
bramki wielo wejściowe. Symbol przykładowej cztero wejściowej bramki AND oraz zależność sygnału wyjściowego od sygnałów wejściowych przedstawia rysunek 2.6.

Układy cyfrowe 37

y = x

Rysunek 2.6. Czterowejściowa bramka AND

2. Suma logiczna - bramka OR.

Tabela 2.7 pokazuje wartości dwuargumentowej sumy logicznej w zależności od wartości jej argumentów, a rysunek 2.7 przedstawia symbol graficzny dwuwejściowej bramki OR realizującej to działanie.

Tabela 2.7. Tabela prawdy dwuwejściowej bramki OR

J ..... ^X1 .	^x2	y
0	0	0
0	1	1
1	0	1
1	1	1

Sumę logiczną zapisujemy jako:

x,vx₂ = y lub x,+x₂ = y

i czytamy jako „x, lub x₂”. Podobnie jak w poprzednim punkcie, możemy działanie to uogólnić na wiele argumentów, podając następujące jej określenie. Suma logiczna jest równa zeru tylko wtedy, gdy wszystkie argumenty są równe 0. W pozostałych przypadkach wynikiem działania jest 1.

Rysunek 2.7. Symbol bramki OR 3. Negacja - bramka NOT.

Operację negacji, czyli zaprzeczenia, oznaczamy następująco: