Capture111

Rozdział 12. Testowanie hipotez — inne statystyki

12.1 Wprowadzenie

proporcji, i skorclo-

W rozdziale 11 omówiliśmy zagadnienia związane ze stosowaniem testów jstotno-sci wobec średnich arytmetycznych. Nierzadko potrzebne bywają równie/, icu, istotności dla proporcji, wariancji, współczynników korelacji czy innych statyki Ogólne uzasadnienie teoretyczne stosowania w tych przypadkach testów istotności jest dokładnie takie samo jak w przypadku średnich arytmetycznych, aczkolwiek procedur)' techniczne szacowania potrzebnych prawdopodobieństw są odmienne W bieżącym rozdziale omawiamy stosowanie testów- istotności wobec wariancji oraz współczynników korelacji przy próbach niezależnych i wanych.

12.2. Istotność różnicy

między dwiema proporcjami niezależnymi

Przy interpretacji wyników badań eksperymentalnych pojawiają się czasami zagadnienia wymagające zastosowania testów istotności różnic między dwiema proporcjami niezależnymi. W tego rodzaju przypadkach wyniki pochodzą / dwóch prób pobranych niezależnie od siebie. Wśród A'| elementów pochodzących z pierwszej próby /| ma cechę A. Wśród AA elementów pochodzących z drugiej prób) /_; ma cechę A Proporcje posiadania cechy A w tych dwóch próbach wynoszą f]/\. = p, ¹    - P: Czy te dwie próby można uważać za próby losowe pobrane / tej samej

populacji? Czy />, różni się w sposób istotny od p{!

Rozpatrzmy przykład. W pewnym badaniu opinii publicznej proporcja 0.65 próby pobranej spośród mieszkańców miasta deklaruje pozytywną postawę wobec pewnego zagadnienia Taką samą postawę deklaruje proporcja 0.55 mieszkańców wsi Czy można twierdzić, ze różnica między tymi proporcjami wskazuje na istnienie różnicy w opinii między miastem a wsią? Weźmy inny przykład Proporcji

_p = t Ul .

Lac/enie wyniKOW z awocn proo w ceiu otrzymania jednego oszacowania p j/Asidniooe jest faktem, że we wszystkich przypadkach, gdy badana jest różnica irj<d/y dwiema proporcjami, zakładamy hipotezę zerowa Zgodnie z la hipoteza ricd/y proporcjami w populacji me ma żadnej różnicy Ponieważ zakładam;, hi-zerowa, możemy zastosować oszacowanie p oparte na połączonych wym-Ubzobu prób. Procedura ta jest analogiczna do procedury, jaka stosowaliśmy w i^cic r różnicy między średnimi przy próbach niezależnych, łącząc sumy kwadra-z dwóch prób w celu otrzymania jednego oszacowania wariancji Aby zbadać różnicę między dwiema proporcjami, dzielimy otrzymana rozmeę nujdiy tymi proporcjami przez oszacowanie błędu standardowego tej różnicy, otrzymując:

P\ ~*PJ _    P\-P2

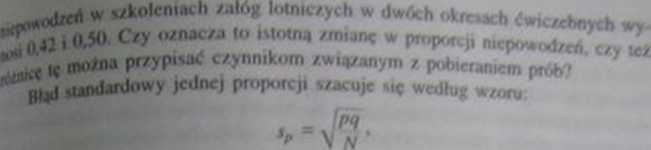
- wartość proporcji / próby.

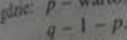
_Bł*i ŁiwBdOWy ^róźnic> ^m,«^d/y *"»«"»■» proporcjami ..partym. _{nj pr((h}^_h ./alcMjcb swcujc się według wzoru:

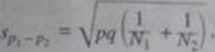
jest OtacowMiem opartym na dwóch próbach połączonych Warto* _P Isicw wę. foto)* ^do *^icbie ^ występowania cech w ..hu pmbach. a ru-!_cf<uc dziel* otrzymana sumę przez liczebność całkowita obu prób Żalem

~ V_M|(iw,) + d/iV_:)i

Warto# z mo/na interpretować jako odchylenie od jednostkowej krzywej nomul-rej pod warunkiem, ze iV, i JV₂ sq dostatecznie duz.e. p zaś nie jest ani bardzo małe. im bardzo duże. Jak zwykle w przypadku testu dwustronnego, wymagane s-t war-lowi l.% i 2.58 dla istotności na poziomie odpowiednio 5 i I procent.

Jak duże powinny być N i jak dalece p powinno odbiegać *h1 wartości skraj-oych. by stosunek ten można było interpretować jako odchylenie od jednostkowej krzywej normalnej? Można tu zastosować dowolni* regułę. Jeżeli mniejsza wartość /•lubę potnnużonu prze/ mniejszy wartość .V przekracza 5. to stosunek ten można

219