082

82

6. Testowanie hipotez

Obliczamy statystyki:

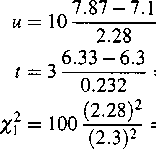
= 98.3,

= 0.375

= 3.384.

2    _ 0.232²

*=¹⁰(0^2F =

Dla pierwszej hipotezy, obszar krytyczny jest dwustronny, symetryczny {—u_a,u_a), gdzie u_a wyznaczamy z zależności 4>(«_a) = 1 - a/2 = 0.975. Stąd u_a = 1.96, a więc należy odrzucić hipotezę zerową.

Dla hipotezy drugiej, podobnie t_a = 2.26, więc nie ma podstaw do odrzucenia hipotezy zerowej. Statystyka X\ ^ma rozkład asymptotycznie normalny N(100, \/200), więc

^-100 _ 98.3-100 \/200 ~    v^/2Ó0

nie należy do obszaru krytycznego i nie odrzucamy hipotezy zerowej. Podobnie dla hipotezy ostatniej, < Xa ⁼ 16.91 i nie odrzucamy hipotezy zerowej.

Chcąc sprawdzić, czy można dokonywać pomiarów parametru metodą pośrednią dzielimy wynik przez y= 1.2 otrzymując nowex'₁ =Xj/y=6.56 i s\ = .v,/y= 1.90. Następnie weryfikujemy hipotezę H₀ : x\ =x₂, zastępując er, przez sj. Weryfikując hipotezę o równości dwóch średnich korzystamy ze statystyki

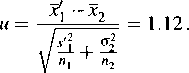
Nie ma więc podstaw do odrzucenia hipotezy o równości średnich, a stąd i do odrzucenia hipotezy o poprawności metody pomiarów pośrednich.

Przykład 6.1.2.

Dla danych z przykładu 5.2.1 zweryfikujmy hipotezę H₀ : m = 1.45 wobec hipotezy alternatywnej H_] :m> 1.45. Przyjmiemy poziom istotności a = 0.01.

Rozwiązanie.

Skorzystamy ze statystyki

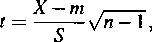
której wartość dla danych z tego przykładu x = 1.501, s = 0.0469 i przy prawdziwości hipotezy H₀ wynosi 3.226. Z tablic wartości krytycznych rozkładu t-Studenta otrzymujemy obszar krytyczny Q = (t_a,°°), czyli taki, że Pr(t > t_a) = 0.01 lub też (co łatwiej